Giải Toán 11 trang 70 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 70 Tập 1 trong Bài 1: Giới hạn của dãy số Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 70.

Giải Toán 11 trang 70 Tập 1 Chân trời sáng tạo

Bài 4 trang 70 Toán 11 Tập 1: Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).

a) Kí hiệu a_n là diện tích của hình vuông thứ n và S_n là tổng diện tích của n hình vuông đầu tiên. Viết công thức tính a_n, S_n (n = 1, 2, 3, ...) và tìm limS_n (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông).

b) Kí hiệu p_n là chu vi của hình vuông thứ n và Q_n là tổng chu vi của n hình vuông đầu tiên. Viết công thức tính p_n và Q_n (n = 1, 2, 3, ...) và tìm limQ_n (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).

Lời giải:

a) Diện tích của các hình vuông lập thành một cấp số nhân lùi vô hạn (a_n) với số hạng đầu là u₁ = 1 và công bội $\frac{1}{2}$ nên công thức tổng quát của a_n = ${\left(\frac{1}{2}\right)}^{n-1}$.

Ta có: $S_n=1+\frac{1}{2}+\frac{1}{4}+\mathrm{...}+\frac{1}{2^n}+\mathrm{...}$

Tổng cấp số nhân lùi vô hạn là: $S=\lim S_n=\lim \left(1+\frac{1}{2}+\frac{1}{4}+\mathrm{...}+\frac{1}{2^n}+\mathrm{...}\right)=\frac{1}{1-\frac{1}{2}}=2$.

b) Chu vi p_n của hình vuông lập thành một cấp số nhân lùi vô hạn với số hạng đầu u₁ = 4 và công bội q = $\frac{1}{2}$ có số hạng tổng quát là: $p_n=4{\left(\frac{1}{2}\right)}^{n-1}$.

Ta có: $Q_n=4+4.\frac{1}{2}+4.\frac{1}{4}+\mathrm{...}+4.\frac{1}{2^n}+\mathrm{...}$

Tổng của cấp số nhân lùi vô hạn là: $Q=\lim Q_n=\lim \left(4+4.\frac{1}{2}+4.\frac{1}{4}+\mathrm{...}+4.\frac{1}{2^n}+\mathrm{...}\right)=\frac{4}{1-\frac{1}{2}}=8$.

Bài 5 trang 70 Toán 11 Tập 1: Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:

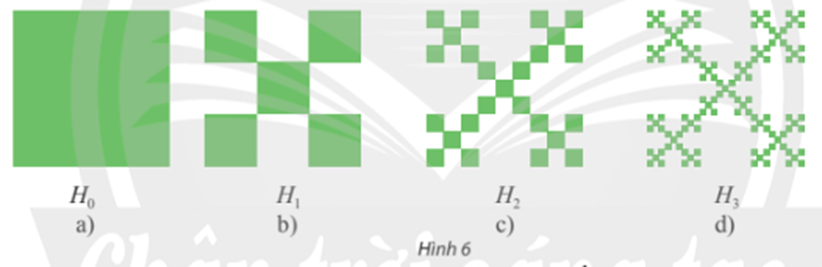
a) Bắt đầu một hình vuông H­₀ cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông H₀ thành chín hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình H₁ (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của H₁ thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình H₂ (xem Hình 6c). Tiếp tục quá trình này ta nhận được một dãy hình H_n(n = 1, 2, 3, ...).

Ta có: H₁ có 5 hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3}$;

H₂ có 5.5 = 5² hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3}.\frac{1}{3}=\frac{1}{3^2};\mathrm{...}$

Từ đó, nhận được H_n có 5ⁿ hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3^n}$.

a) Tính diện tích S_n của H_n và tính lim S_n.

b) Tính chu vi p_n của H_n và tính limp_n.

(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích lim S_n và chu vi limp_n).

Lời giải:

a) Diện tích S_n của H_n là $S_n=5^n.{\left(\frac{1}{3}\right)}^n.{\left(\frac{1}{3}\right)}^n=5^n.{\left(\frac{1}{3}\right)}^{2n}={\left(\frac{5}{9}\right)}^n$

Khi đó ${\text{limS}}_n=\lim {\left(\frac{5}{9}\right)}^n=0$.

b) Chu vi p_n của H_n là: $p_n=5^n.\left(4.\frac{1}{3^n}\right)=4.{\left(\frac{5}{3}\right)}^n$.

Khi đó limp_n = lim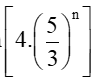 = 0.

Lời giải bài tập Toán 11 Bài 1: Giới hạn của dãy số Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 64

• Giải Toán 11 trang 65

• Giải Toán 11 trang 66

• Giải Toán 11 trang 68

• Giải Toán 11 trang 69