Đặt log25 = a, log35 = b. Khi đó, log65 tính theo a và b bằng

Cho hai số thực dương x, y và hai số thực α, β tùy ý. Khẳng định nào sau đây là sai?

Rút gọn biểu thức  $\sqrt{x\sqrt{x\sqrt{x}}}:x^{\frac{5}{8}}\left(x>0\right)$ ta được

Cho hai số thực dương a, b với a ≠ 1. Khẳng định nào sau đây là đúng?

Cho bốn số thực dương a, b, x, y với a, b ≠ 1. Khẳng định nào sau đây là sai?

Cho hàm số y = 2^x. Khẳng định nào sau đây là sai?

Hàm số nào sau đây đồng biến trên tập xác định của nó?

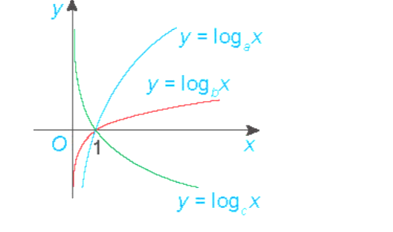
Cho đồ thị ba hàm số y = log_ax, y = log_bx và y = log_cx như hình bên. Mệnh đề nào sau đây là đúng?

Cho 0 < a ≠ 1. Tính giá trị của biểu thức  $B={\log }_a\left(\frac{a^2\cdot \sqrt[3]{a}\cdot \sqrt[5]{a^4}}{\sqrt[4]{a}}\right)+a^{2{\log }_a\frac{\sqrt{105}}{30}}$.