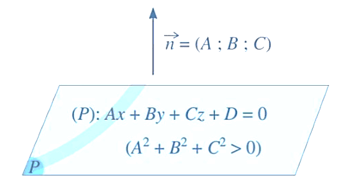Lý thuyết Toán lớp 12 Phương trình mặt phẳng - Cánh diều

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 1: Phương trình mặt phẳng sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Phương trình mặt phẳng - Cánh diều

Lý thuyết Phương trình mặt phẳng

1. Vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng

1.1. Vectơ pháp tuyến

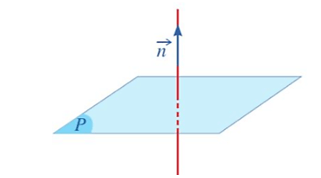
Cho mặt phẳng (P). Nếu vectơ $\overrightarrow{n}$  khác $\overrightarrow{0}$  và có giá vuông góc với mặt phẳng (P) thì $\overrightarrow{n}$  được gọi là vectơ pháp tuyến của mặt phẳng (P).

Nhận xét: Nếu $\overrightarrow{n}$  là một vectơ pháp tuyến của một mặt phẳng thì k$\overrightarrow{n}$ (k ≠ 0) cũng là một vectơ pháp tuyến của mặt phẳng đó.

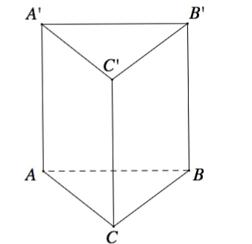
Ví dụ 1. Cho hình lăng trụ đứng ABC.A'B'C'. Tìm một vectơ pháp tuyến của mặt phẳng (ABC).

Hướng dẫn giải

Vì ABC.A'B'C' là lăng trụ đứng nên AA' ⊥ (ABC).

Vậy $\overrightarrow{A{A}^{\text{'}}}$ là một vectơ pháp tuyến của mặt phẳng (ABC).

1.2. Cặp vectơ chỉ phương

Cho mặt phẳng (P). Hai vectơ không cùng phương có giá song song hoặc nằm trong mặt phẳng (P) được gọi là cặp vectơ chỉ phương của mặt phẳng (P).

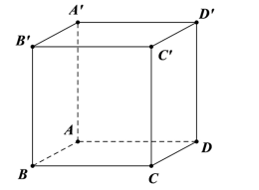
Ví dụ 2. Cho hình lập phương ABCD.A'B'C'D'. Tìm một cặp vectơ chỉ phương của mặt phẳng (ABCD).

Hướng dẫn giải

Do hai vectơ $\overrightarrow{BA}$ , $\overrightarrow{BC}$  không cùng phương và có giá nằm trong mặt phẳng (ABCD) nên $\overrightarrow{BA}$ , $\overrightarrow{BC}$ là một cặp vectơ chỉ phương của mặt phẳng (ABCD).

1.3. Xác định vectơ pháp tuyến của mặt phẳng khi biết cặp vectơ chỉ phương

Nếu hai vectơ $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$ ,$\overrightarrow{b}=\left(b_1;b_2;b_3\right)$ là cặp vectơ chỉ phương của mặt phẳng (P) thì $\overrightarrow{n}=\left[\overrightarrow{a},\overrightarrow{b}\right]=\left(\left|\begin{array}{cc}{a}_2& a_3\\ b_2& b_3\end{array}\right|;\left|\begin{array}{cc}{a}_3& a_1\\ b_3& b_1\end{array}\right|;\left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|\right)$ là một vectơ pháp tuyến của mặt phẳng (P).

Ví dụ 3. Cho mặt phẳng (P) có cặp vectơ chỉ phương là $\overrightarrow{u}=\left(0;-1;3\right)$ và $\overrightarrow{v}=\left(5;0;1\right)$ . Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (P).

Hướng dẫn giải

Một vectơ pháp tuyến của mặt phẳng (P) là:

$\overrightarrow{n}=\left[\overrightarrow{u},\overrightarrow{v}\right]=\left(\left|\begin{array}{cc}-1& 3\\ 0& 1\end{array}\right|;\left|\begin{array}{cc}3& 0\\ 1& 5\end{array}\right|;\left|\begin{array}{cc}0& -1\\ 5& 0\end{array}\right|\right)=\left(-1;15;5\right)$.

2. Phương trình tổng quát của mặt phẳng

● Trong không gian với hệ tọa độ Oxyz, mỗi mặt phẳng (P) có phương trình dạng Ax + By + Cz + D = 0, trong đó A, B, C không đồng thời bằng 0;

● Ngược lại, mỗi phương trình Ax + By + Cz + D = 0, trong đó A, B, C không đồng thời bằng 0, đều xác định một mặt phẳng trong không gian với hệ tọa độ Oxyz.

→ Phương trình Ax + By + Cz + D = 0 (A, B, C không đồng thời bằng 0) là phương trình tổng quát của mặt phẳng. Hệ số D gọi là hệ số tự do của phương trình tổng quát.

Nhận xét: Ta có thể chứng minh rằng nếu mặt phẳng (P) có phương trình tổng quát là Ax + By + Cz + D = 0, trong đó A, B, C không đồng thời bằng 0, thì vectơ $\overrightarrow{n}=\left(A;B;C\right)$ là một vectơ pháp tuyến của mặt phẳng (P).

Ví dụ 4. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình 3x + 2y – z + 4 = 0. Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (P).

Hướng dẫn giải

Ta có 3x + 2y – z + 4 = 0 ⇔ 3 ∙ x + 2 ∙ y + (– 1) ∙ z + 4 = 0.

Mặt phẳng (P) nhận $\overrightarrow{n}=\left(3;2;-1\right)$  làm vectơ pháp tuyến.

3. Lập phương trình tổng quát của mặt phẳng biết một số điều kiện

3.1. Lập phương trình tổng quát của mặt phẳng đi qua một điểm và biết vectơ pháp tuyến

Mặt phẳng (P) đi qua điểm I(x₀; y₀; z₀) và nhận $\overrightarrow{n}=\left(A;B;C\right)$  làm vectơ pháp tuyến có phương trình tổng quát là:

Ax + By + Cz + D = 0 với D = − Ax₀ − By₀ − Cz₀.

Chú ý: Mặt phẳng (P) đi qua điểm I(x₀; y₀; z₀) và nhận $\overrightarrow{n}=\left(A;B;C\right)$  làm vectơ pháp tuyến có phương trình là:

A(x – x₀) + B(y – y_0­) + C(z – z₀) = 0.

Ví dụ 5. Lập phương trình mặt phẳng (P) đi qua điểm I(0; 1; 2) và nhận $\overrightarrow{n}=\left(2;3;-1\right)$ làm vectơ pháp tuyến.

Hướng dẫn giải

Mặt phẳng (P) có phương trình là:

2(x – 0) + 3(y – 1) – 1(z – 2) = 0 $\iff$ 2x + 3y – z – 1 = 0.

3.2. Lập phương trình tổng quát của mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương

Để lập phương trình mặt phẳng (P) đi qua điểm I(x₀; y₀; z₀) có cặp vectơ chỉ phương là $\overrightarrow{u},\overrightarrow{v}$ , ta có thể làm như sau:

Bước 1. Tìm $\overrightarrow{n}=\left[\overrightarrow{u},\overrightarrow{v}\right]$ .

Bước 2. Lập phương trình mặt phẳng (P) đi qua điểm I(x₀; y₀; z₀) nhận $\overrightarrow{n}$ làm vectơ pháp tuyến.

Ví dụ 6. Lập phương trình mặt phẳng (P) đi qua điểm I(1; 3; − 2) có cặp vectơ chỉ phương là $\overrightarrow{u}=\left(2;-1;3\right),\overrightarrow{v}=\left(3;2;-3\right)$ .

Hướng dẫn giải

Xét vectơ $\overrightarrow{n}=\left[\overrightarrow{u},\overrightarrow{v}\right]=\left(\left|\begin{array}{cc}-1& 3\\ 2& -3\end{array}\right|;\left|\begin{array}{cc}3& 2\\ -3& 3\end{array}\right|;\left|\begin{array}{cc}2& -1\\ 3& 2\end{array}\right|\right)$ , tức là $\overrightarrow{n}$  = (− 3; 15; 7). Khi đó, $\overrightarrow{n}$  là vectơ pháp tuyến của mặt phẳng (P).

Vậy mặt phẳng (P) có phương trình là:

− 3(x – 1) + 15(y – 3) + 7(z + 2) = 0 ⇔ 3x – 15y – 7z + 28 = 0

3.3. Lập phương trình tổng quát của mặt phẳng đi qua ba điểm không thẳng hàng

Để lập phương trình mặt phẳng (P) đi qua ba điểm H(a₁; b₁; c₁), I(a₂; b₂; c₂), K(a₃; b₃; c₃) không thẳng hàng, ta có thể làm như sau:

Bước 1. Tìm cặp vectơ chỉ phương của mặt phẳng (P) là:

$\overrightarrow{HI}$ = (a₂ – a₁; b₂ – b₁; c₂ – c₁), $\overrightarrow{HK}$  = (a₃ – a₁; b₃ – b₁; c₃ – c₁).

Bước 2. Tìm $\overrightarrow{n}=\left[\overrightarrow{HI},\overrightarrow{HK}\right]$ .

Bước 3. Lập phương trình mặt phẳng (P) đi qua điểm H(a₁; b₁; c₁) nhận $\overrightarrow{n}$  làm vectơ pháp tuyến.

Ví dụ 7. Lập phương trình mặt phẳng (Q) đi qua ba điểm A(1; 0; −2), B(1; 1; 1) và C(0; −1; 2).

Hướng dẫn giải

Ta có: $\overrightarrow{AB}=\left(0;1;3\right)$ , $\overrightarrow{AC}=\left(-1;-1;4\right)$ .

Xét vectơ $\overrightarrow{n}$ = $\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(\left|\begin{array}{cc}1& 3\\ -1& 4\end{array}\right|;\left|\begin{array}{cc}3& 0\\ 4& -1\end{array}\right|;\left|\begin{array}{cc}0& 1\\ -1& -1\end{array}\right|\right)$ , tức là $\overrightarrow{n}$ = (7; – 3; 1).

Khi đó, $\overrightarrow{n}$  là vectơ pháp tuyến của mặt phẳng (Q).

Vậy mặt phẳng (Q) có phương trình là:

7(x – 1) – 3(y – 0) + 1(z + 2) = 0 ⇔ 7x – 3y + z – 5 = 0.

Chú ý: Mặt phẳng đi qua ba điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) với abc ≠ 0 có phương trình là:

$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$.

Phương trình đó còn được gọi là phương trình mặt phẳng theo đoạn chắn.

4. Điều kiện song song, vuông góc của hai mặt phẳng

4.1. Điều kiện song song của hai mặt phẳng

Cho mặt phẳng (P₁) có phương trình tổng quát là A₁x + B₁y + C₁z + D₁ = 0

và mặt phẳng (P₂) có phương trình tổng quát là A₂x + B₂y + C₂z + D₂ = 0.

Gọi $\overrightarrow{n_1}=\left(A_1;B_1;C_1\right)$ , $\overrightarrow{n_2}=\left(A_2;B_2;C_2\right)$  lần lượt là vectơ pháp tuyến của hai mặt phẳng (P₁), (P₂).

Khi đó: (P₁) // (P₂) khi và chỉ khi tồn tại số thực k ≠ 0 sao cho $\left\{\begin{array}{l}\overrightarrow{n_1}=k\overrightarrow{n_2}\\ D_1\ne k{D}_2\end{array}\right.$ .

Ví dụ 8. Cho hai mặt phẳng (P₁): 3x + y – 4z + 8 = 0, (P₂): 6x + 2y – 8z + 3 = 0.

Chứng minh rằng (P₁) // (P₂).

Hướng dẫn giải

Hai mặt phẳng (P₁), (P₂) có vectơ pháp tuyến lần lượt là

$\overrightarrow{n_1}$ = (3; 1; – 4), $\overrightarrow{n_2}$  = (6; 2; – 8).

Do $\overrightarrow{n_2}=2\overrightarrow{n_1}$  và D₂ ≠ 2D₁ (vì D₁ = 8 và D₂ = 3) nên (P₁) // (P₂).

4.2. Điều kiện vuông góc của hai mặt phẳng

Cho mặt phẳng (P₁) có phương trình tổng quát là A₁x + B₁y + C₁z + D₁ = 0 và mặt phẳng (P₂) có phương trình tổng quát là A₂x + B₂y + C₂z + D₂ = 0. Khi đó:

(P₁) $\perp$(P₂) $\iff$ A₁A₂ + B₁B₂ + C₁C₂ = 0.

Ví dụ 9. Cho hai mặt phẳng (P): x + 2y + z + 1 = 0 và (Q): 3x – 2y + z + 5 = 0. Chứng minh rằng hai mặt phẳng (P) và (Q) vuông góc với nhau.

Hướng dẫn giải

Hai mặt phẳng (P) và (Q) có vectơ pháp tuyến lần lượt là $\overrightarrow{n_P}=\left(1;2;1\right),\overrightarrow{n_Q}=\left(3;-2;1\right)$ .

Vì $\overrightarrow{n_P}\cdot \overrightarrow{n_Q}$  = 1 ∙ 3 + 2 ∙ (– 2) + 1 ∙ 1 = 0 nên $\overrightarrow{n_P}\perp \overrightarrow{n_Q}$ . Vậy (P) $\perp$ (Q).

5. Khoảng cách từ một điểm đến một mặt phẳng

Khoảng cách từ điểm M₀(x₀; y₀; z₀) đến mặt phẳng (P):

Ax + By + Cz + D = 0 (A² + B² + C² > 0)

được tính theo công thức: $d\left(M_0,\left(P\right)\right)=\frac{\left|A{x}_0+B{y}_0+C{z}_0+D\right|}{\sqrt{A^2+B^2+C^2}}$ .

Ví dụ 10. Cho mặt phẳng (P): x + 2y – 2z + 8 = 0 và điểm I(−1; 2; 1). Tính khoảng cách từ điểm I đến mặt phẳng (P).

Hướng dẫn giải

Khoảng cách từ điểm I đến mặt phẳng (P) là:

$d\left(I,\left(P\right)\right)=\frac{\left|-1+2\cdot 2-2\cdot 1+8\right|}{\sqrt{1^2+2^2+{\left(-2\right)}^2}}=\frac{9}{3}=3$

Bài tập Phương trình mặt phẳng

Bài 1. Phương trình nào sau đây là phương trình tổng quát của mặt phẳng?

A. 3x – y + z² + 2 = 0.

B. x – y² + 2x – 3 = 0.

C. x² – y + 3z + 1 = 0.

D. 2x + 3y + 4z – 1 = 0.

Hướng dẫn giải

Đáp án đúng là: D

Phương trình tổng quát của mặt phẳng có dạng Ax + By + Cz + D = 0 với A, B, C không đồng thời bằng 0 và x, y, z có số mũ bằng 1.

Nhận thấy chỉ có phương trình 2x + 3y + 4z – 1 = 0 đúng dạng phương trình tổng quát của mặt phẳng.

Bài 2. Cho mặt phẳng (P) có phương trình 3x + 2y – z + 4 = 0. Mặt phẳng (P) có một vectơ pháp tuyến là:

A. $\overrightarrow{n}=\left(3;2;1\right)$ .

B. $\overrightarrow{n}=\left(-2;3;1\right)$ .

C. $\overrightarrow{n}=\left(3;2;-1\right)$ .

D. $\overrightarrow{n}=\left(3;-2;-1\right)$ .

Hướng dẫn giải

Đáp án đúng là: C

Mặt phẳng (P): 3x + 2y – z + 4 = 0 có một vectơ pháp tuyến là $\overrightarrow{n}=\left(3;2;-1\right)$ .

Bài 3. Lập phương trình mặt phẳng (P) trong mỗi trường hợp sau:

a) (P) đi qua điểm A(1; 2; 3) và nhận $\overrightarrow{n}$ = (4; 3; – 1) làm vectơ pháp tuyến;

b) (P) đi qua ba điểm H(1; 0; 0), I(0; 2; 0) và K(0; 0; 3).

Hướng dẫn giải

a) Phương trình mặt phẳng (P) là:

4(x – 1) + 3(y – 2) – 1(z – 3) = 0 ⇔ 4x + 3y – z – 7 = 0.

b) Phương trình mặt phẳng (P) là:

$\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1$ ⇔ 6x + 3y + 2z – 6 = 0.

Bài 4.

a) Lập phương trình mặt phẳng (P) đi qua điểm M(1; 1; − 1) và nhận hai vectơ $\overrightarrow{u}=\left(2;5;-2\right)$ và $\overrightarrow{v}=\left(1;-3;2\right)$ làm cặp vectơ chỉ phương.

b) Tính khoảng cách từ điểm A(1; 2; 0) đến mặt phẳng (P) vừa lập được ở câu a.

Hướng dẫn giải

a) Xét vectơ $\overrightarrow{n}=\left[\overrightarrow{u},\overrightarrow{v}\right]=\left(\left|\begin{array}{cc}5& -2\\ -3& 2\end{array}\right|;\left|\begin{array}{cc}-2& 2\\ 2& 1\end{array}\right|;\left|\begin{array}{cc}2& 5\\ 1& -3\end{array}\right|\right)$ , tức là $\overrightarrow{n}$  = (4; − 6; − 11).

Khi đó, $\overrightarrow{n}$  là vectơ pháp tuyến của mặt phẳng (P).

Vậy mặt phẳng (P) có phương trình là:

4(x – 1) – 6(y – 1) – 11(z + 1) = 0 ⇔ 4x – 6y – 11z – 9 = 0.

b) Khoảng cách từ điểm A đến mặt phẳng (P) là:

$d\left(A,\left(P\right)\right)=\frac{\left|4\cdot 1-6\cdot 2-11\cdot 0-9\right|}{\sqrt{4^2+{\left(-6\right)}^2+{\left(-11\right)}^2}}=\frac{17}{\sqrt{173}}$.

Bài 5. Một công trình đang xây dựng được gắn hệ trục Oxyz (đơn vị trên mỗi trục tọa độ là mét). Ba bức tường (P), (Q), (R) (như hình vẽ) của tòa nhà lần lượt có phương trình (P): x + 2y – 2z + 1 = 0, (Q): 2x + y + 2z – 3 = 0, (R): 2x + 4y – 4z – 19 = 0.

a) Hãy kiểm tra tính song song hoặc vuông góc giữa các bức tường (P), (Q), (R) của tòa nhà.

b) Tính khoảng cách giữa hai bức tường (P) và (R) của tòa nhà.

Hướng dẫn giải

a) Các mặt phẳng (P), (Q), (R) có vectơ pháp tuyến lần lượt là

$\overrightarrow{n_P}=\left(1;2;-2\right),\overrightarrow{n_Q}=\left(2;1;2\right),\overrightarrow{n_R}=\left(2;4;-4\right)$.

Ta có:

+) $\overrightarrow{n_P}\cdot \overrightarrow{n_Q}=1\cdot 2+2\cdot 1+\left(-2\right)\cdot 2=0$ . Do đó, (P) ⊥ (Q).

+) $\overrightarrow{n_Q}\cdot \overrightarrow{n_R}=2\cdot 2+1\cdot 4+2\cdot \left(-4\right)=0$ . Do đó, (Q) ^ (R).

+) $\left\{\begin{array}{l}\overrightarrow{n_R}=2\overrightarrow{n_P}\\ -19\ne 2\cdot 1\end{array}\right.$  nên (P) // (R).

b) Lấy A(−1; 0; 0) Î (P).

Vì (P) // (R) nên d((P), (R))= d(A, (R)) = $\frac{\left|2\cdot \left(-1\right)+4\cdot 0-4\cdot 0-19\right|}{\sqrt{2^2+4^2+{\left(-4\right)}^2}}=\frac{21}{6}=\frac{7}{2}$

Học tốt Phương trình mặt phẳng

Các bài học để học tốt Phương trình mặt phẳng Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 1: Phương trình mặt phẳng