Lý thuyết Toán lớp 12 Phương trình mặt cầu - Cánh diều

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 3: Phương trình mặt cầu sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Phương trình mặt cầu - Cánh diều

Lý thuyết Phương trình mặt cầu

1. Định nghĩa mặt cầu

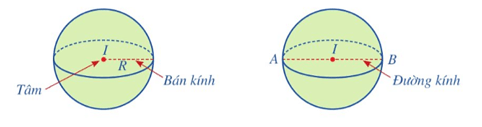
Cho trước điểm I và số dương R. Mặt cầu tâm I bán kính R là tập hợp tất cả các điểm trong không gian cách điểm I một khoảng bằng R.

Nhận xét

+ Điểm M thuộc mặt cầu tâm I bán kính R khi và chỉ khi IM = R.

+ Điểm M nằm trong mặt cầu tâm I bán kính R khi và chỉ khi IM < R.

+ Điểm M nằm ngoài mặt cầu tâm I bán kính R khi và chỉ khi IM > R.

Ví dụ 1. Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 4) và mặt cầu tâm I đi qua điểm A(4; 3; 2). Tính bán kính của mặt cầu đó.

Hướng dẫn giải

Vì mặt cầu tâm I đi qua điểm A nên điểm A thuộc mặt cầu tâm I, do đó bán kính của mặt cầu tâm I là R = IA.

Ta có IA = $\sqrt{{\left(4-1\right)}^2+{\left(3-2\right)}^2+{\left(2-4\right)}^2}=\sqrt{14}$.

Vậy bán kính của mặt cầu đã cho là R = $\sqrt{14}$ .

2. Phương trình mặt cầu

Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu tâm I(a; b; c) bán kính R là:

(x – a)² + (y – b)² + (z – c)² = R².

Ví dụ 2. Viết phương trình mặt cầu có tâm I(1; 4; 3) bán kính R = 5.

Hướng dẫn giải

Phương trình mặt cầu tâm I(1; 4; 3) bán kính R = 5 là:

(x – 1)² + (y – 4)² + (z – 3)² = 25.

Nhận xét:

● Cho mặt cầu tâm I(a; b; c) bán kính R có phương trình là:

(x – a)² + (y – b)² + (z – c)² = R².

Ta có thể viết phương trình đó về dạng:

x² + y² + z² – 2ax – 2by – 2cz + d = 0 với d = a² + b² + c² – R².

Vậy mỗi mặt cầu đều có phương trình dạng: x² + y² + z² – 2ax – 2by – 2cz + d = 0.

● Ngược lại, xét phương trình có dạng: x² + y² + z² – 2ax – 2by – 2cz + d = 0.

Ta có: x² + y² + z² – 2ax – 2by – 2cz + d = 0

⇔ x² – 2ax + a² + y² – 2by + b² + z² – 2cz + c² = a² + b² + c² – d

⇔ (x – a)² + (y – b)² + (z – c)² = a² + b² + c² – d.

Do đó, phương trình x² + y² + z² – 2ax – 2by – 2cz + d = 0 xác định một mặt cầu khi và chỉ khi a² + b² + c² – d > 0. Ngoài ra, nếu a² + b² + c² – d > 0 thì phương trình đó xác định mặt cầu tâm I(a; b; c) và bán kính $R=\sqrt{a^2+b^2+c^2-d}$ .

Ví dụ 3. Trong không gian với hệ tọa độ Oxyz, phương trình nào trong các phương trình sau là phương trình của mặt cầu. Xác định tâm và bán kính của mặt cầu ứng với phương trình đó.

a) x² + y² + z² + x – 2y + 4z – 3 = 0;

b) x² + y² + z² + 2x + 4y – 4z + 12 = 0;

c) 2x² + y² + 2z² – 2x + 2y – 2z + 1 = 0.

Hướng dẫn giải

a) Phương trình đã cho tương ứng với $a=-\frac{1}{2}$ ; b = 1; c = −2 và d = −3.

Có a² + b² + c² – d = $\frac{33}{4}>0$ .

Do đó, đây là phương trình mặt cầu với tâm $I\left(-\frac{1}{2};1;-2\right);R=\frac{\sqrt{33}}{2}$.

b) Phương trình đã cho tương ứng với a = −1; b = −2; c = 2; d = 12.

Có a² + b² + c² – d = −3 < 0 nên đây không phải là phương trình của một mặt cầu.

c) Phương trình đã cho không phải là phương trình của một mặt cầu vì các hệ số của x² và y² khác nhau.

Bài tập Phương trình mặt cầu

Bài 1. Cho mặt cầu có phương trình: (x – 1)² + (y – 3)² + (z + 2)² = 5. Đường kính của mặt cầu đó bằng

A. $\sqrt{5}$.

B. 10.

C. $2\sqrt{5}$ .

D. 2,5.

Hướng dẫn giải

Đáp án đúng là: C

Mặt cầu đã cho có bán kính $R=\sqrt{5}$ . Suy ra đường kính của mặt cầu đó là $2\sqrt{5}$ .

Bài 2. Tâm của mặt cầu (S): (x – 3)² + (y + 1)² + (z – 2)² = 4 có tọa độ là

A. (−3; 1; −2).

B. (−4; 2; −6).

C. (4; −2; 6).

D. (3; −1; 2).

Hướng dẫn giải

Đáp án đúng là: D

Ta có (x – 3)² + (y + 1)² + (z – 2)² = 4 ⇔ (x – 3)² + [y – (– 1)]² + (z – 2)² = 2². 

Vậy mặt cầu (S) có tâm I(3; −1; 2).

Bài 3. Lập phương trình mặt cầu (S) trong mỗi trường hợp sau:

a) (S) có tâm I(1; – 3; 5) bán kính 4.

b) (S) có tâm I(2; 1; 0), đi qua điểm A(0; 1; 2).

c) (S) có đường kính AB với A(1; 2; 5), B(7; 4; −3).

Hướng dẫn giải

a) Phương trình mặt cầu (S) có tâm I(1; – 3; 5) bán kính 4 là:

(x – 1)² + (y + 3)² + (z – 5)² = 16.

b) Ta có bán kính R = IA = $\sqrt{{\left(0-2\right)}^2+{\left(1-1\right)}^2+{\left(2-0\right)}^2}=2\sqrt{2}$ .

Phương trình mặt cầu (S) là: (x – 2)² + (y – 1)² + z² = 8.

c) Gọi I là trung điểm của AB. Khi đó tọa độ của điểm I là:

$x_I=\frac{1+7}{2}=4;y_I=\frac{2+4}{2}=3;z_I=\frac{5+\left(-3\right)}{2}=1$. Suy ra I(4; 3; 1).

Ta có bán kính $R=\frac{AB}{2}=\frac{\sqrt{{\left(7-1\right)}^2+{\left(4-2\right)}^2+{\left(-3-5\right)}^2}}{2}=\sqrt{26}$ .

Phương trình mặt cầu (S) là: (x – 4)² + (y – 3)² + (z – 1)² = 26.

Bài 4. Cho mặt cầu (S) có phương trình: x² + (y – 2)² + (z + 3)² = 36.

a) Xác định tọa độ tâm I và tính bán kính R của mặt cầu (S).

b) Điểm A(0; 2; 3) có thuộc mặt cầu (S) hay không?

c) Điểm B(1; – 4; 5) nằm trong hay nằm ngoài mặt cầu (S)?

d) Điểm C(2; 2; – 4) nằm trong hay nằm ngoài mặt cầu (S)?

Hướng dẫn giải

a) Ta có x² + (y – 2)² + (z + 3)² = 36 ⇔ (x – 0)² + (y – 2)² + [z – (– 3)]² = 6².

Do đó, mặt cầu (S) có tâm I(0; 2; – 3), bán kính R = 6.

b)

Cách 1: Ta có IA =$\sqrt{{\left(0-0\right)}^2+{\left(2-2\right)}^2+{\left(3-\left(-3\right)\right)}^2}=6$  = R.

Do đó, điểm A(0; 2; 3) thuộc mặt cầu (S).

Cách 2: Thay tọa độ điểm A vào phương trình mặt cầu (S), ta được:

0² + (2 – 2)² + (3 + 3)² = 36.

Vậy điểm A(0; 2; 3) thuộc mặt cầu (S).

c) Ta có IB = $\sqrt{{\left(1-0\right)}^2+{\left(-4-2\right)}^2+{\left(5-\left(-3\right)\right)}^2}=\sqrt{101}$  > 6 = R.

Vậy điểm B(1; – 4; 5) nằm ngoài mặt cầu (S).

d) Ta có IC = $\sqrt{{\left(2-0\right)}^2+{\left(2-2\right)}^2+{\left(-4-\left(-3\right)\right)}^2}=\sqrt{5}$  < 6 = R.

Vậy điểm C(2; 2; – 4) nằm trong mặt cầu (S).

Bài 5. Cho mặt cầu (S) có phương trình: x² + y² + z² – 2x – 2y – 2z – 22 = 0 và mặt phẳng (P) có phương trình: 3x – 2y + 6z + 14 = 0. Tính khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (P).

Hướng dẫn giải

Ta có x² + y² + z² – 2x – 2y – 2z – 22 = 0

⇔ x² – 2x + 1 + y² – 2y + 1 + z² – 2z + 1 = 25

⇔ (x – 1)² + (y – 1)² + (z – 1)² = 25

Do đó, mặt cầu (S) có tâm I(1; 1; 1).

Vậy khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (P) là:

$d\left(I,\left(P\right)\right)=\frac{\left|3\cdot 1-2\cdot 1+6\cdot 1+14\right|}{\sqrt{3^2+{\left(-2\right)}^2+6^2}}=\frac{21}{7}=3$.

Bài 6. Trong không gian hệ trục tọa độ Oxyz (đơn vị trên mỗi trục là kilômét) một trạm phát sóng rađa của Nga được đặt trên bán đảo Crimea ở vị trí I(−2; 1; −1) và được thiết kế phát hiện máy bay của địch ở khoảng cách tối đa 500 km.

a) Sử dụng phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phủ sóng của rađa trong không gian.

b) Hai chiếc máy bay do thám của Mỹ và Anh đang bay ở vị trí có tọa độ lần lượt là M(−200; 100; −250) và N(350; −100; 300). Hỏi rađa của Nga có thể phát hiện ra hai chiếc máy bay do thám của Mỹ và Anh không?

Hướng dẫn giải

a) Mặt cầu mô tả ranh giới bên ngoài vùng phủ sóng của rađa trong không gian là mặt cầu tâm I(−2; 1; −1) bán kính R = 500 và có phương trình là:

[x – (– 2)]² + (y – 1)² + [z – (– 1)]² = 500² ⇔ (x + 2)² + (y – 1)² + (z + 1)² = 250 000.

b) Có $IM=\sqrt{{\left(-200+2\right)}^2+{\left(100-1\right)}^2+{\left(-250+1\right)}^2}\approx 333,18<R$ .

$IN=\sqrt{{\left(350+2\right)}^2+{\left(-100-1\right)}^2+{\left(300+1\right)}^2}\approx 474,03<R$.

Vậy rađa của Nga có thể phát hiện ra hai chiếc máy bay do thám của Mỹ và Anh.

Học tốt Phương trình mặt cầu

Các bài học để học tốt Phương trình mặt cầu Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 3: Phương trình mặt cầu