Lý thuyết Toán 12 Cánh diều Học kì 1 (hay, chi tiết)

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Học kì 1 Cánh diều hay nhất, chi tiết bám sát nội dung từng bài học sgk Toán 12 Tập 1 sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm Toán 12.

Lý thuyết Toán 12 Học kì 1 - Cánh diều

Lý thuyết Tính đơn điệu của hàm số

1. Tính đơn điệu của hàm số

* Tính đơn điệu và dấu của đạo hàm

Cho hàm số y = f(x) có đạo hàm trên tập K ⊂ ℝ, trong đó K là một khoảng, đoạn hoặc nửa khoảng.

- Nếu f'(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.

- Nếu f'(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

Chú ý: Nếu hàm số y = f(x) đồng biến trên tập K hoặc nghịch biến trên tập K thì hàm số y = f(x) còn được gọi là đơn điệu trên K ⊂ ℝ.

Ví dụ 1. Xét dấu y' rồi tìm khoảng đồng biến, nghịch biến của hàm số

y = x³ – 2x² + x + 1.

Hướng dẫn giải

Hàm số đã cho có tập xác định là ℝ.

Ta có y' = 3x² – 4x + 1;

y' = 0 ⇔ 3x² – 4x + 1 = 0 ⇔ $x=\frac{1}{3}$ hoặc x = 1.

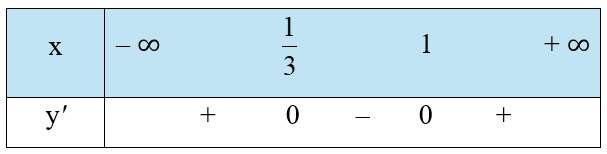
Ta có bảng xét dấu của y' như sau:

Vậy hàm số đồng biến trên mỗi khoảng $\left(-\infty ;\frac{1}{3}\right)$ và (1; + ∞); nghịch biến trên khoảng $\left(\frac{1}{3};1\right)$ .

* Cho hàm số y = f(x) có đạo hàm trên tập K ⊂ ℝ trong đó K là một khoảng, đoạn hoặc nửa khoảng. Nếu f'(x) ≥ 0 (hoặc f'(x) ≤ 0) với mọi x thuộc K và f'(x) = 0 chỉ tại một số hữu hạn điểm của K thì hàm số f(x) đồng biến (hoặc nghịch biến) trên K.

Ví dụ 2. Tìm các khoảng đơn điệu của hàm số y = $\frac{1}{5}$x⁵ –$\frac{2}{3}$x³ + x + 4.

Hướng dẫn giải

Hàm số đã cho có tập xác định là ℝ.

Ta có y' = x⁴ – 2x² + 1 = (x² – 1)² = (x – 1)² ∙ (x + 1)²;

y' ≥ 0 với mọi x ∈ ℝ và y' = 0 ⇔ x = – 1 hoặc x = 1.

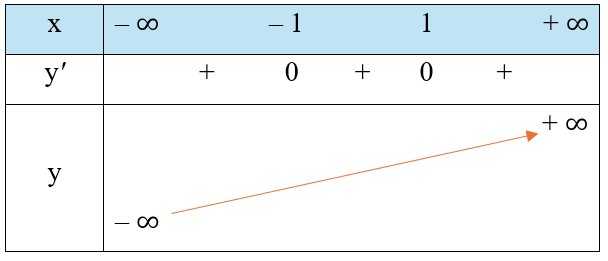
Bảng biến thiên của hàm số như sau:

Vậy hàm số đồng biến trên khoảng (– ∞; + ∞).

* Các bước xét tính đồng biến, nghịch biến của hàm số y = f(x)

Bước 1. Tìm tập xác định của hàm số y = f(x).

Bước 2. Tính đạo hàm f'(x). Tìm các điểm x_i (i = 1, 2, …, n) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.

Bước 3. Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên.

Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Ví dụ 3. Tìm các khoảng đơn điệu của hàm số $y=\frac{x-1}{2x+1}$

Hướng dẫn giải

Hàm số đã cho có tập xác định là ℝ \ $\left(-\frac{1}{2}\right)$

Ta có $y^{\text{'}}=\frac{3}{{\left(2x+1\right)}^2};$ y' > 0 với mọi $x\ne -\frac{1}{2}$

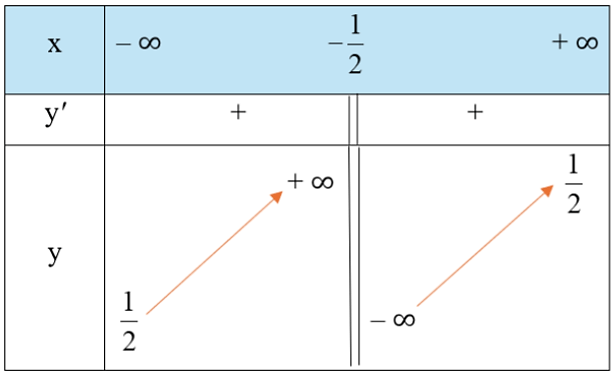
Bảng biến thiên của hàm số như sau:

Vậy hàm số đồng biến trên mỗi khoảng $\left(-\infty ;-\frac{1}{2}\right)$ và $\left(-\frac{1}{2};+\infty \right)$

2. Điểm cực trị, giá trị cực trị của hàm số

* Định nghĩa

Cho hàm số y = f(x) liên tục trên tập K ⊂ ℝ, trong đó K là một khoảng, đoạn hoặc nửa khoảng và x­₀ ∈ K, x₁ ∈ K.

- x₀ được gọi là một điểm cực đại của hàm số đã cho nếu tồn tại một khoảng (a; b) chứa điểm x₀ sao cho (a; b) ⊂ K và f(x) < f(x₀) với mọi x ∈ (a; b) và x ≠ x₀.

Khi đó, f(x₀) được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là f_CĐ.

- x₁ được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng (c; d) chứa điểm x₁ sao cho (c; d) ⊂ K và f(x) > f(x₁) với mọi x ∈ (c; d) và x ≠ x₁.

Khi đó, f(x₁) được gọi là giá trị cực tiểu của hàm số đã cho, kí hiệu là f_CT.

- Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị).

Chú ý: Nếu x₀ là một điểm cực trị của hàm số y = f(x) thì người ta nói rằng hàm số y = f(x) đạt cực trị tại điểm x₀. Khi đó, điểm M(x₀; f(x₀)) được gọi là điểm cực trị của đồ thị hàm số y = f(x).

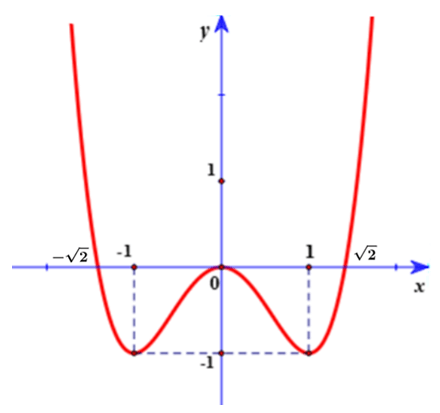
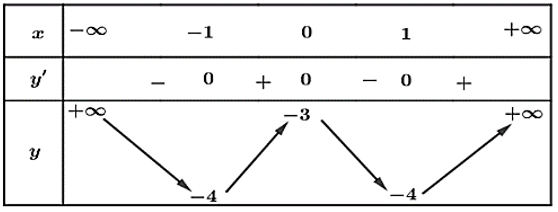
Ví dụ 4. Cho đồ thị hàm số y = f(x) như hình dưới đây.

Hãy chỉ ra các điểm cực trị của hàm số đó.

Hướng dẫn giải

- Xét khoảng $\left(-\sqrt{2};0\right)$ chứa điểm x = – 1. Quan sát đồ thị hàm số y = f(x) ở hình trên, ta thấy f(x) > f(– 1) với mọi x ∈ $\left(-\sqrt{2};0\right)$ và x ≠ – 1.

Do vậy x = – 1 là một điểm cực tiểu của hàm số y = f(x).

- Xét khoảng (– 1; 1) chứa điểm x = 0. Quan sát đồ thị hàm số y = f(x) ở hình trên, ta thấy f(x) < f(0) với mọi x ∈ (– 1; 1) và x ≠ 0.

Do vậy x = 0 là điểm cực đại của hàm số y = f(x).

- Xét khoảng $\left(0;\sqrt{2}\right)$ chứa điểm x = 1. Quan sát đồ thị hàm số y = f(x) ở hình trên, ta thấy f(x) > f(1) với mọi x ∈ $\left(0;\sqrt{2}\right)$ và x ≠ 1.

Do vậy x = 1 là một điểm cực tiểu của hàm số y = f(x).

* Mối liên hệ giữa đạo hàm và cực trị

Giả sử hàm số y = f(x) liên tục trên khoảng (a; b) chứa điểm x₀ và có đạo hàm trên các khoảng (a; x₀) và (x₀; b). Khi đó

- Nếu f'(x) < 0 với mọi x ∈ (a; x₀) và f'(x) > 0 với mọi x ∈ (x₀; b) thì hàm số f(x) đạt cực tiểu tại điểm x₀.

- Nếu f'(x) > 0 với mọi x ∈ (a; x₀) và f'(x) < 0 với mọi x ∈ (x₀; b) thì hàm số f(x) đạt cực đại tại điểm x₀.

Ví dụ 5. Tìm điểm cực trị của hàm số y = x⁴ – 2x² – 3.

Hướng dẫn giải

Hàm số đã cho có tập xác định là ℝ.

Ta có y' = 4x³ – 4x;

y' = 0 ⇔ 4x³ – 4x = 0 ⇔ x = – 1 hoặc x = 0 hoặc x = 1.

Bảng biến thiên của hàm số như sau:

Vậy hàm số đạt cực đại tại điểm x = 0 và đạt cực tiểu tại các điểm x = – 1, x = 1.

* Các bước tìm điểm cực trị của hàm số f(x)

Bước 1. Tìm tập xác định của hàm số f(x):

Bước 2. Tính đạo hàm f'(x). Tìm các điểm x_i (i = 1, 2, …, n) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.

Bước 3. Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên.

Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các điểm cực trị của hàm số.

Ví dụ 6. Tìm điểm cực trị (nếu có) của mỗi hàm số sau:

a) y = – x³ + 3x² + 4;

b) $y=\frac{2x+1}{x-2}$

Hướng dẫn giải

a) y = – x³ + 3x² + 4

Hàm số đã cho có tập xác định là ℝ.

Ta có y' = – 3x² + 6x;

y' = 0 ⇔ – 3x² + 6x = 0 ⇔ x = 0 hoặc x = 2.

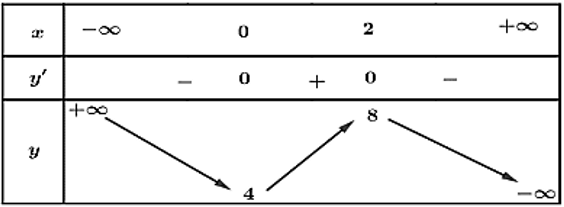
Bảng biến thiên của hàm số như sau:

Vậy hàm số đạt cực đại tại điểm x = 2 và đạt cực tiểu tại điểm x = 0.

b) $y=\frac{2x+1}{x-2}$

Hàm số đã cho có tập xác định là ℝ \ {2}.

Ta có $y^{\text{'}}=\frac{-5}{{\left(x-2\right)}^2};$ y' < 0 với mọi x ≠ 2.

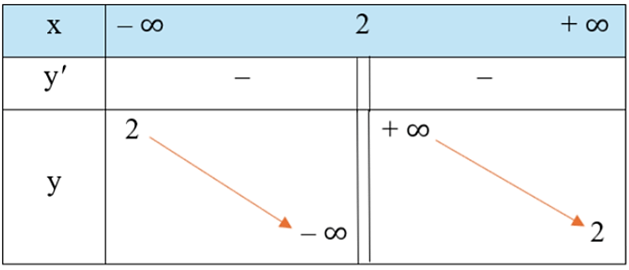
Bảng biến thiên của hàm số như sau:

Vậy hàm số không có điểm cực trị.

................................

................................

................................