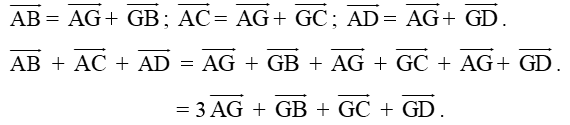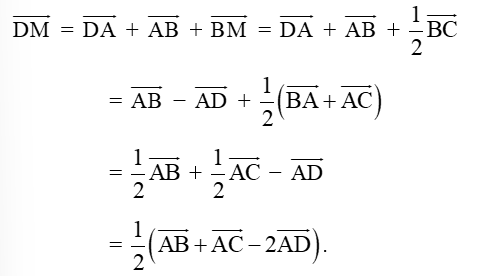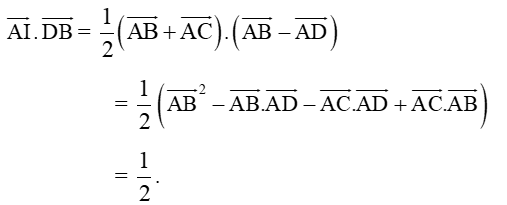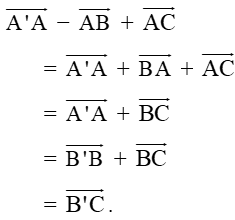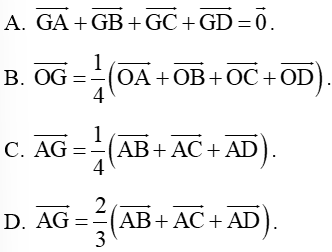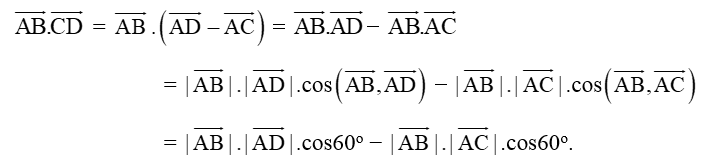Lý thuyết Toán lớp 12 Vectơ và các phép toán vectơ trong không gian - Cánh diều

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 1: Vectơ và các phép toán vectơ trong không gian sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Vectơ và các phép toán vectơ trong không gian - Cánh diều

Lý thuyết Vectơ và các phép toán vectơ trong không gian

A. Lý thuyết

1. Khái niệm vectơ trong không gian

• Vectơ trong không gian

Vectơ trong không gian là một đoạn thẳng có hướng.

Chú ý:

Cho đoạn thẳng AB trong không gian. Nếu ta chọn điểm đầu là A, điểm cuối là B thì ta có một vectơ, kí hiệu là $\overrightarrow{AB}$ , đọc là “vectơ AB”.

Khi không cần chỉ rõ điểm đầu và điểm cuối của vectơ, vectơ còn được kí hiệu là $\overrightarrow{a}$, $\overrightarrow{b}, \overrightarrow{u }, \overrightarrow{v},$...

• Các khái niệm có liên quan đến vectơ trong không gian như: giá của vectơ, độ dài của vectơ, vectơ cùng phương, vectơ cùng hướng, vectơ – không, hai vectơ bằng nhau, hai vectơ đối nhau, … được phát biểu tương tự như trong mặt phẳng.

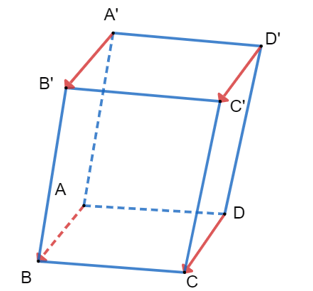
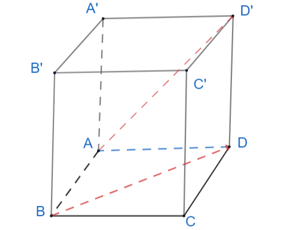
Ví dụ 1. Cho hình hộp ABCD.A'B'C'D'. Hãy chỉ ra ba vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp sao cho mỗi vectơ đó:

a) Bằng vectơ $\overrightarrow{DC}$.

b) Là vectơ đối của vectơ $\overrightarrow{DC}$.

Hướng dẫn giải

a) Do các vectơ $\overrightarrow{D\text{'}C\text{'}}$,$\overrightarrow{AB}$,$\overrightarrow{A\text{'}B\text{'}}$ cùng hướng với vectơ $\overrightarrow{DC}$ và

 DC = D'C' = A'B' = AB (tính chất hình hộp) nên $\overrightarrow{DC}$ = $\overrightarrow{D\text{'}C\text{'}}$= $\overrightarrow{AB}$ = $\overrightarrow{A\text{'}B\text{'}}$ .

Vậy ba vectơ $\overrightarrow{D\text{'}C\text{'}}$,$\overrightarrow{AB}$,$\overrightarrow{A\text{'}B\text{'}}$  có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vectơ $\overrightarrow{DC}$ .

b) Do các vectơ $\overrightarrow{C\text{'}D\text{'}},\overrightarrow{BA}, \overrightarrow{B\text{'}A\text{'}}$ ngược hướng với vectơ $\overrightarrow{DC}$  và

DC = D'C' = A'B' = AB (tính chất hình hộp) nên ba vectơ $\overrightarrow{C\text{'}D\text{'}},\overrightarrow{BA}, \overrightarrow{B\text{'}A\text{'}}$   là ba vectơ đối của vectơ $\overrightarrow{DC}$ .

Chú ý:  

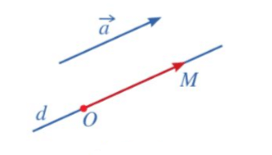
Cho điểm O và vectơ $\overrightarrow{a}$ . Khi đó, tồn tại duy nhất điểm M trong không gian sao cho $\overrightarrow{OM}=\overrightarrow{a}$ .

Để xác định điểm M, ta làm như sau (xem hình dưới):

• Qua O kẻ đường thẳng d song song hoặc trùng với giá của vectơ $\overrightarrow{a}$.

• Lấy điểm M trên đường thẳng d sao cho hai vectơ $\overrightarrow{OM}$,$\overrightarrow{a}$ là cùng hướng và độ dài đoạn thẳng OM bằng độ dài đoạn thẳng vectơ $\overrightarrow{a}$.

2. Các phép toán vectơ trong không gian

2.1. Tổng và hiệu của hai vectơ trong không gian

 - Tổng của hai vectơ

Trong không gian, cho hai vectơ $\overrightarrow{a}, \overrightarrow{\mathbf{b}}$. Lấy một điểm A tùy ý, vẽ $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{BC}=\overrightarrow{b}$.

Vectơ $\overrightarrow{AC}$ được gọi là tổng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu là $\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}$.

Chú ý:

• Phép lấy tổng hai vectơ còn được gọi là phép cộng vectơ.

• Phép cộng vectơ trong không gian cũng có các tính chất như phép cộng vectơ trong mặt phẳng, chẳng hạn: Phép cộng vectơ trong không gian cũng có các tính chất giao hoán, kết hợp, cộng với vectơ – không. Do đó, ta cũng định nghĩa được tổng của ba vectơ trong không gian.

• Khi thực hiện phép cộng vectơ trong không gian, ta vẫn có thể áp dụng quy tắc ba điểm, quy tắc hình bình hành như đối với vectơ trong mặt phẳng.

Đối với vectơ trong không gian, ta cũng có các quy tắc sau:

• Với ba điểm A, B, C trong không gian, ta có: $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ (quy tắc ba điểm);

• Nếu ABCD là hình bình hành thì $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ (quy tắc hình bình hành).

• Nếu ABCD.A'B'C'D' là hình hộp thì $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA\text{'}}=\overrightarrow{AC\text{'}}$ (quy tắc hình hộp).

Ví dụ 2: Cho tứ diện ABCD. Chứng minh rằng: $\overrightarrow{AC}+\overrightarrow{DB}=\overrightarrow{AB}+\overrightarrow{DC}$.

Hướng dẫn giải

Theo quy tắc ba điểm, ta có:

$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$.

Do đó:

$\overrightarrow{AC} + \overrightarrow{DB} = \overrightarrow{AB} +\overrightarrow{BC}+ \overrightarrow{DB}$

                  = $\overrightarrow{AB} + \left(\overrightarrow{DB}+\overrightarrow{BC}\right)$

                  = $\overrightarrow{AB} + \overrightarrow{DC}$

Vậy $\overrightarrow{AC} + \overrightarrow{DB} = \overrightarrow{AB} + \overrightarrow{DC}$ (đpcm).

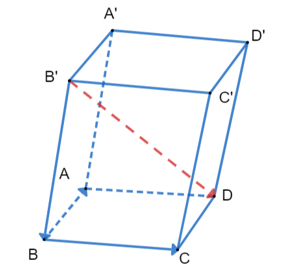
Ví dụ 3: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: $\overrightarrow{B\text{'}B} +\overrightarrow{BC}+ \overrightarrow{BA} = \overrightarrow{B\text{'}D}$.

Hướng dẫn giải

Ta có: $\overrightarrow{BC} = \overrightarrow{B\text{'}C\text{'}},\overrightarrow{BA} = \overrightarrow{B\text{'}A\text{'}}$.

Do đó: $\overrightarrow{B\text{'}B} + \overrightarrow{BC} + \overrightarrow{BA} = \overrightarrow{B\text{'}B} + \overrightarrow{B\text{'}C\text{'}}+ \overrightarrow{B\text{'}A\text{'}} = \overrightarrow{B\text{'}D}$ (quy tắc hình hộp).

- Hiệu của hai vectơ

• Trong không gian, cho hai vectơ $\overrightarrow{a}, \overrightarrow{b}$. Hiệu của vectơ $\overrightarrow{a}$ và vectơ $\overrightarrow{b}$ là tổng của vectơ $\overrightarrow{a}$với vectơ đối của vectơ $\overrightarrow{b}$, kí hiệu là $\overrightarrow{a}-\overrightarrow{b}$.

Phép lấy hiệu của hai vectơ còn được gọi là phép trừ vectơ.

Đối với vectơ trong không gian, ta có quy tắc sau:

• Với ba điểm O, A, B trong không gian, ta có: $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}$ (quy tắc hiệu).

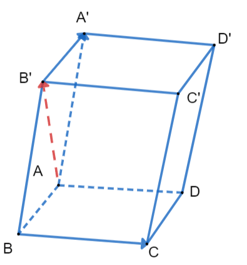
Ví dụ 4: Cho hình hộp ABCD.A'B'C'D'. Chứng minh $\overrightarrow{AA\text{'}}-\overrightarrow{B\text{'}A\text{'}}= \overrightarrow{AB\text{'}}$.

Hướng dẫn giải:

Ta có: $\overrightarrow{AA\text{'}}- \overrightarrow{B\text{'}A\text{'}}= \overrightarrow{AA\text{'}}+ \left(-\overrightarrow{B\text{'}A\text{'}}\right)$

                                 = $\overrightarrow{AA\text{'}} + \overrightarrow{A\text{'}B\text{'}}$

                                 = $\overrightarrow{AB\text{'}}$.

Vậy $\overrightarrow{AA\text{'}} - \overrightarrow{B\text{'}A\text{'}}=\overrightarrow{AB\text{'}}$ (đpcm).

2.2. Tích của một số với một vectơ trong không gian

Tương tự như trong mặt phẳng, trong không gian ta cũng có định nghĩa sau:

Cho số thực k ≠ 0 và vectơ $\overrightarrow{a} \ne \overrightarrow{0}$. Tích của số k với vectơ $\overrightarrow{a}$ là một vectơ, kí hiệu là $k\overrightarrow{a}$, được xác định như sau:

• Cùng hướng với vectơ $\overrightarrow{a}$ nếu k > 0, ngược hướng với vectơ $\overrightarrow{a}$ nếu k < 0;

• Có độ dài bằng |k| . | $\overrightarrow{a}$|.

Quy ước: 0.$\overrightarrow{a}$ = $\overrightarrow{0}$, k. $\overrightarrow{0}$ = $\overrightarrow{0}$ . Do đó, k.$\overrightarrow{a}$ = $\overrightarrow{0}$ khi và chỉ khi k = 0 hoặc $\overrightarrow{a}$= $\overrightarrow{0}$ .

Chú ý:

• Phép lấy tích của một số với một vectơ gọi là phép nhân một số với một vectơ.

• Phép nhân một số với một vectơ trong không gian có các tính chất sau:

Với hai vectơ bất kì $\overrightarrow{a}$ ,$\overrightarrow{b}$ và hai số thực h, k ta có:

+ k($\overrightarrow{a}$ + $\overrightarrow{b}$) = k $\overrightarrow{a}$ + k$\overrightarrow{b}$ ; k($\overrightarrow{a}$- $\overrightarrow{b}$ ) = k$\overrightarrow{a}$  − k$\overrightarrow{b}$ ;

+ (h + k)$\overrightarrow{a}$  = h $\overrightarrow{a}$ + k $\overrightarrow{a}$;

+ h(k $\overrightarrow{a}$) = (hk) $\overrightarrow{a}$;

+ 1$\overrightarrow{a}$ =$\overrightarrow{a}$ ; (−1) $\overrightarrow{a}$ = − $\overrightarrow{a}$.

• Hai vectơ $\overrightarrow{a}$, $\overrightarrow{b}$ khác $\overrightarrow{0}$ là cùng phương khi và chỉ khi có một số thực k ≠ 0 sao cho $\overrightarrow{a}=k\overrightarrow{b}$ .

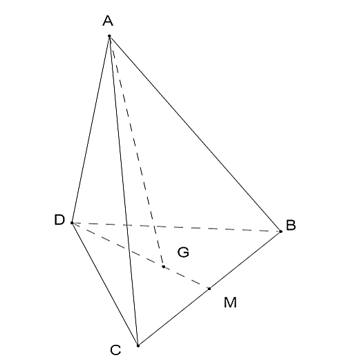
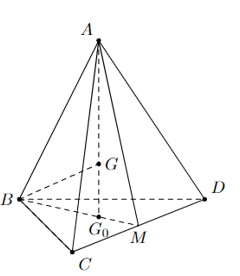
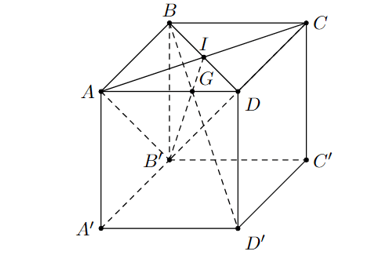
Ví dụ 5: Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD, M là trung điểm của BC. Chứng minh rằng:

a) $\overrightarrow{AG}= \frac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)$ ;

b) $\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}-2\overrightarrow{AD}\right)= \overrightarrow{DM}$.

Hướng dẫn giải:

a) Ta có:

Vì G là trọng tâm của tam giác BCD nên $\overrightarrow{GB}+ \overrightarrow{GC} +\overrightarrow{GD}$= $\overrightarrow{0}$.

Do đó, ta có: $\overrightarrow{AB} +\overrightarrow{AC}+ \overrightarrow{AD}=3\overrightarrow{AG}$ ⇔$\overrightarrow{AG}=\frac{1}{3} \left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)$.

⇒ đpcm.

b) Vì M là trung điểm BC nên suy ra $\overrightarrow{BM} =\frac{1}{2}\overrightarrow{BC}$.

Ta có

⇒ đpcm.

2.3. Tích vô hướng của hai vectơ trong không gian

Trong không gian, cho hai vectơ $\overrightarrow{a}$,$\overrightarrow{b}$ khác $\overrightarrow{0}$. Lấy một điểm O tùy ý và vẽ hai vectơ $\overrightarrow{OA}=\overrightarrow{a}$, $\overrightarrow{OB}=\overrightarrow{b}$. Góc giữa hai vectơ $\overrightarrow{a}$,$\overrightarrow{b}$  trong không gian là góc giữa hai vectơ $\overrightarrow{OA},$$\overrightarrow{OB}$, kí hiệu là $\left(\overrightarrow{a},\overrightarrow{b}\right)$ .

Chú ý: 0^o ≤ $\left(\overrightarrow{a},\overrightarrow{b}\right)$  ≤ 180^o.

Ví dụ 6: Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa hai vectơ $\left(\overrightarrow{AD\text{'}},\overrightarrow{BD}\right)$ .

Hướng dẫn giải:

Ta có: $\left(\overrightarrow{AD\text{'}},\overrightarrow{BD}\right) =\left(\overrightarrow{BC\text{'}},\overrightarrow{BD}\right)= \widehat{C\text{'}BD}$.

Do tam giác C'BD là tam giác đều nên $\widehat{C\text{'}BD}$ = 60^o.

Vậy $\left(\overrightarrow{AD\text{'}},\overrightarrow{BD}\right)$ = 60^o.

• Trường hợp tổng quát, ta có định nghĩa sau:

Trong không gian, cho hai vectơ $\overrightarrow{a}$,$\overrightarrow{b}$  khác $\overrightarrow{0}$ . Tích vô hướng của hai vectơ $\overrightarrow{a}$và $\overrightarrow{b}$ , kí hiệu $\overrightarrow{a}.\overrightarrow{b}$, là một số thực được xác định bởi công thức  $\overrightarrow{a}.\overrightarrow{b}$= | $\overrightarrow{a}$|.| $\overrightarrow{b}$|.cos($\overrightarrow{a}$, $\overrightarrow{b}$) ở đó

($\overrightarrow{a}$ ,$\overrightarrow{b}$) là góc giữa hai vectơ $\overrightarrow{a}$,$\overrightarrow{b}$.

Quy ước: Tích vô hướng của một vectơ bất kì với vectơ $\overrightarrow{0}$ bằng 0.

Chú ý:

•Tích vô hướng của hai vectơ trong không gian có tính chất sau:

Với các vectơ bất kì$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$ và số thực k tùy ý, ta có:

+ $\overrightarrow{a}$. $\overrightarrow{b}$ = $\overrightarrow{b}$ . $\overrightarrow{a}$ (tính chất giao hoán);

+$\overrightarrow{a}$ .($\overrightarrow{b}$+ $\overrightarrow{c}$) = $\overrightarrow{a}$. $\overrightarrow{b}$ +$\overrightarrow{a}$ .$\overrightarrow{c}$  (tính chất phân phối);

+ (k$\overrightarrow{a}$ ).$\overrightarrow{b}$ = k($\overrightarrow{a}$ . $\overrightarrow{b}$) = $\overrightarrow{a}$ (k$\overrightarrow{b}$);

+${\overrightarrow{a}}^2$≥ 0, trong đó ${\overrightarrow{a}}^2$ = $\overrightarrow{a}$ .$\overrightarrow{a}$ . Ngoài ra, ${\overrightarrow{a}}^2$ = 0 ⇔ $\overrightarrow{a}$= .$\overrightarrow{0}$

• Nếu $\overrightarrow{a}$ ,$\overrightarrow{b}$  là hai vectơ khác  thì cos($\overrightarrow{a}$ ,$\overrightarrow{b}$ ) = $\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}$ .

Ví dụ 7:

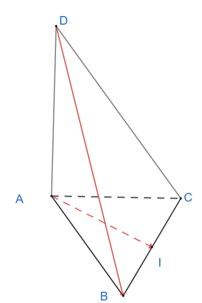
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc và AB = AC = AD = 1. Gọi I là trung điểm của cạnh BC. Tính góc giữa vectơ $\overrightarrow{AI}$ và $\overrightarrow{DB}.$

Hướng dẫn giải:

Theo đề, ta có: $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|$= 1 và $\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AC}.\overrightarrow{AD}=\overrightarrow{AD}.\overrightarrow{AB}$ = 0.

Ta có cos $\left(\overrightarrow{AI},\overrightarrow{DB}\right)$ = $\frac{\overrightarrow{AI}.\overrightarrow{DB}}{\left|\overrightarrow{AI}\right|.\left|\overrightarrow{DB}\right|}$ .

Mặt khác, do $\overrightarrow{AI}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)$ và $\overrightarrow{DB}=\overrightarrow{AB}-\overrightarrow{AD}$

nên

Lại có $\left|\overrightarrow{AI}\right|=\frac{\sqrt{2}}{2}$; $\left|\overrightarrow{DB}\right|=\sqrt{2}$.

Do đó cos $\left(\overrightarrow{AI},\overrightarrow{DB}\right)$= $\frac{\overrightarrow{AI}.\overrightarrow{DB}}{\left|\overrightarrow{AI}\right|.\left|\overrightarrow{DB}\right|}=\frac{\frac{1}{2}}{\frac{\sqrt{2}}{2}.\sqrt{2}}=\frac{1}{2}$.

Vậy $\left(\overrightarrow{AI},\overrightarrow{DB}\right)$= 60^o

Bài tập Vectơ và các phép toán vectơ trong không gian

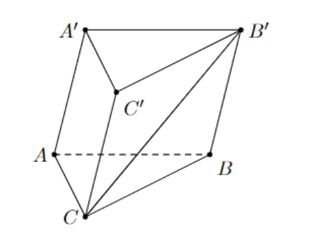
Bài 1: Cho hình lăng trụ ABC.A'B'C'. Vectơ $\overrightarrow{u} =\overrightarrow{A\text{'}A}- \overrightarrow{AB}+ \overrightarrow{AC}$ bằng vectơ nào dưới đây?

Lời giải

Đáp án đúng là: B

Ta có:  

Bài 2: Cho hình tứ diện ABCD có trọng tâm G, điểm O tùy ý. Mệnh đề nào sau đây là sai?

Lời giải

Đáp án đúng là: D

Vì G là trọng tâm của tứ diện ABCD nên ta có $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$.

Khi đó, với mọi vị trí điểm O, ta có: $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=4\overrightarrow{OG}$ .

Chọn O ≡ A, ta được: $\overrightarrow{AA}+\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=4\overrightarrow{AG}$  ⇔ $\overrightarrow{AG}=\frac{1}{4}\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)$ .

Vậy mệnh đề sai là: $\overrightarrow{AG}=\frac{2}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)$ .

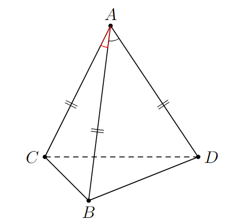
Bài 3: Cho tứ diện ABCD có AB = AC = AD và  $\widehat{BAC}=\widehat{BAD}$= 60^o. Tính góc $\left(\overrightarrow{AB},\overrightarrow{CD}\right)$ .

Lời giải

Ta có:

Mà AC = AD = AB ⇒ $\overrightarrow{AB}.\overrightarrow{CD}$ = 0 ⇒ $\left(\overrightarrow{AB},\overrightarrow{CD}\right)$ = 90^o.

Bài 4: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi G là trọng tâm của tam giác AB'C. Chứng minh $\overrightarrow{BD\text{'}}=3\overrightarrow{BG}$

Lời giải

Cách 1: Gọi I là tâm của hình vuông ABCD

=⇒ I là trung điểm của BD.

Ta có: ∆BIG ∽ ∆ D'B'G

      ⇒$\frac{BG}{D\text{'}G}=\frac{BI}{D\text{'}B\text{'}}=\frac{1}{2}$ ⇒ $\frac{BG}{BD\text{'}}=\frac{1}{3}$= ⇒ $\overrightarrow{BD\text{'}}=3\overrightarrow{BG}$=.

Cách 2: Theo quy tắc hình hộp, ta có: $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB\text{'}}$ = $\overrightarrow{BD\text{'}}$. (1)

Do G là trọng tâm tam giác AB'C nên $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB\text{'}}$ = $3\overrightarrow{BG}$. (2)

Từ (1) và (2) suy ra: $\overrightarrow{BD\text{'}}=3\overrightarrow{BG}$.

⇒ đpcm.

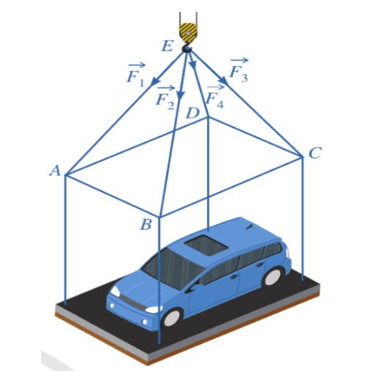
Bài 5: Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD, mặp phẳng (ABCD) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng 30^o. Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng.

Tính trọng lượng của chiếc xe ô tô (làm tròn trên hàng đơn vị). Biết rằng các lực căng $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3};\overrightarrow{F_4}$đều có cường độ là 4 500 N và trọng lượng của khung sắt là 2 500 N.

Lời giải

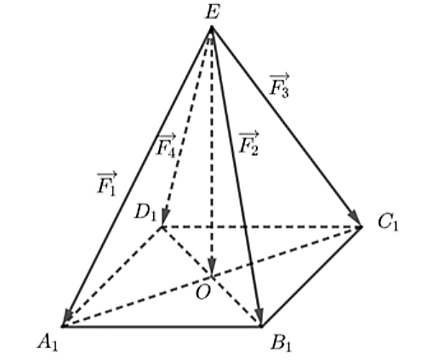
Gọi A₁; B₁; C₁; D₁ lần lượt là các điểm sao cho:

Vì EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng 30^o nên EA₁, EB₁, EC₁, ED₁ bằng nhau và cùng tạo với mặt phẳng (A₁B₁C₁D₁) một góc 30^o_.

Vì ABCD là hình chữ nhật nên A₁B₁C₁D₁ cũng là hình chữ nhật.

Gọi O là tâm của hình chữ nhật A₁B₁C₁D₁.

Suy ra EO ⊥ (A₁B₁C₁D₁).

Do đó, góc giữa đường thẳng EA₁ và mặt phẳng (A₁B₁C₁D₁) bằng góc EA₁O.

Suy ra $\widehat{E{A}_{1}O}$== 30_­^o.

Ta có: |$\overrightarrow{F_1}$=| = | $\overrightarrow{F_2}$=| = | $\overrightarrow{F_3}$=| = | $\overrightarrow{F_4}$=| = 4 500 (N)

Nên EA₁ = EB₁ = EC₁ = ED₁ = 4 500.

Tam giác EOA₁ vuông tại O nên EO = EA₁.sin $\widehat{E{A}_{1}O}$= = 4 500.sin30^o = 2 250 (N).

Theo quy tắc ba điểm, ta có:

$\overrightarrow{E{A}_1}=\overrightarrow{EO}+\overrightarrow{O{A}_1}$=, $\overrightarrow{E{B}_1}=\overrightarrow{EO}+\overrightarrow{O{B}_1}$ =,

= $\overrightarrow{E{C}_1}=\overrightarrow{EO}+\overrightarrow{O{C}_1}$$\overrightarrow{E{D}_1}=\overrightarrow{EO}+\overrightarrow{O{D}_1}$=.

Vì O là trung điểm của A₁C₁ và B₁D₁ nên $\overrightarrow{O{A}_1}+\overrightarrow{O{C}_1}=\overrightarrow{0}$ =, $\overrightarrow{O{B}_1}+\overrightarrow{O{D}_1}=\overrightarrow{0}$ =.

Từ đó suy ra: $\overrightarrow{E{A}_1}+\overrightarrow{E{B}_1}+\overrightarrow{E{C}_1}+\overrightarrow{E{D}_1}=4\overrightarrow{EO}$ =.

                      $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}+\overrightarrow{F_4}=4\overrightarrow{EO}$ =.

Do đó, vì chiếc khung sắt chứa xe ô tô ở vị trí cân bằng nên $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}+\overrightarrow{F_4}=\overrightarrow{P}$ =, ở đó là trọng lực tác dụng lên khung sắt chứa xe ô tô.

Suy ra trọng lượng của khung sắt chứa chiếc xe ô tô là:

| $\overrightarrow{P}$=| = 4| $\overrightarrow{EO}$=| = 4. 2 250 = 9 000 (N).

Vì trọng lượng khung sắt là 2 500 N nên trọng lượng của chiếc ô tô là:

9 000 – 2 500 = 6 500 (N).

Học tốt Vectơ và các phép toán vectơ trong không gian

Các bài học để học tốt Vectơ và các phép toán vectơ trong không gian Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 1: Vectơ và các phép toán vectơ trong không gian