Bài 2 trang 36 Toán 12 Tập 1 Chân trời sáng tạo
Cho hàm số y = x – 3x + 2.
Giải Toán 12 Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản - Chân trời sáng tạo
Bài 2 trang 36 Toán 12 Tập 1: Cho hàm số y = x3 – 3x2 + 2.
a) Tìm điểm I thuộc đồ thị hàm số biết hoành độ của I là nghiệm của phương trình y" = 0.
b) Chứng minh rằng I là trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số.
Lời giải:
a) Xét hàm số y = x3 – 3x2 + 2. Tập xác định của hàm số là D = ℝ.
Ta có y' = 3x2 – 6x; y" = 6x – 6;
y" = 0 ⇔ x = 1.
Với x = 1, ta có y(1) = 0.
Vậy I(1; 0).
b) Ta có y' = 0 ⇔ 3x2 – 6x = 0 ⇔ x = 0 hoặc x = 2.
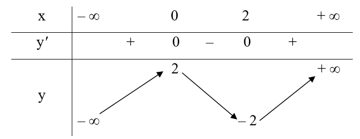
Bảng biến thiên:
Do đó, hàm số đạt cực đại tại x = 0, giá trị cực đại là yCĐ = 2; hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là yCT = – 2.
Hai điểm cực trị của đồ thị hàm số là (0; 2) và (2; – 2).
Ta thấy . Vậy điểm I(1; 0) là trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số.
Lời giải bài tập Toán 12 Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản hay, chi tiết khác:
Hoạt động khám phá trang 25 Toán 12 Tập 1: Cho hàm số y = – x2 + 4x – 3. ....
Thực hành 1 trang 28 Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: ....
Thực hành 2 trang 30 Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: ....
Thực hành 3 trang 32 Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: ....