Thực hành 4 trang 35 Toán 12 Tập 1 Chân trời sáng tạo
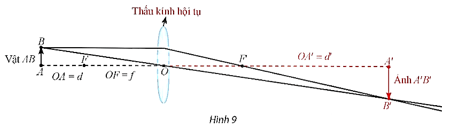
Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f > 0. Gọi d là khoảng cách từ vật đến thấu kính (d > 0), d' là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d' > 0, ảnh ảo thì d'
Giải Toán 12 Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản - Chân trời sáng tạo
Thực hành 4 trang 35 Toán 12 Tập 1: Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f > 0. Gọi d là khoảng cách từ vật đến thấu kính (d > 0), d' là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d' > 0, ảnh ảo thì d' < 0). Ta có công thức:
hay .
(Vật lí 11, Nhà xuất bản Giáo dục Việt Nam, 2012, trang 182, 187).
Xét trường hợp f = 3, đặt x = d, y = d'. Ta có hàm số và x ≠ 3.
a) Khảo sát và vẽ đồ thị của hàm số trên.
b) Dựa vào đồ thị hàm số trên, hãy cho biết vị trí của vật để ảnh của vật là: ảnh thật, ảnh ảo.
c) Khi vật tiến gần đến tiêu điểm thì ảnh thay đổi như thế nào?
Lời giải:
a) Vì d > 0 nên với x = d thì x > 0.
Xét hàm số với x > 0 và x ≠ 3.
1. Tập xác định: D = (0; 3) ∪ (3; + ∞).
2. Sự biến thiên:
● Chiều biến thiên:
Đạo hàm y' = . Vì y' < 0 với mọi x > 0 và x ≠ 3 nên hàm số nghịch biến trên mỗi khoảng (0; 3) và (3; + ∞).
● Tiệm cận:
Ta có . Suy ra đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số.
Ta có . Suy ra đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số.
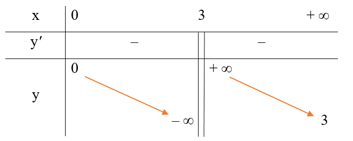
● Bảng biến thiên:
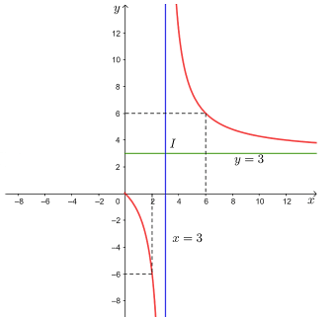
3. Đồ thị:
Đồ thị hàm số đi qua điểm (2; – 6) và điểm (6; 6).
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.
b)
● Để vật là ảnh thật thì d' > 0, tức là y > 0.
Quan sát đồ thị hàm số , ta thấy trên khoảng (3; + ∞), đồ thị hàm số nằm phía trên trục Ox nên y > 0 trên khoảng này. Vậy với x > 3, tức d > 3 hay khoảng cách từ vật đến thấy kính lớn hơn 3 thì ảnh của vật là ảnh thật.
● Để vật là ảnh ảo thì d' < 0, tức là y < 0.
Quan sát đồ thị hàm số , ta thấy trên khoảng (0; 3), đồ thị hàm số nằm phía dưới trục Ox nên y < 0 trên khoảng này. Vậy với x ∈ (0; 3), tức d ∈ (0; 3) hay khoảng cách từ vật đến thấu kính lớn hơn 0 và nhỏ hơn 3 thì ảnh của vật là ảnh ảo.
c) Khi vật tiến gần đến tiêu điểm, tức vị trí A tiến gần đến vị trí F, thì khoảng cách AF dần tiến tới 0, hay d – f → 0, suy ra d → f, tức là x → 3.
Lời giải bài tập Toán 12 Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản hay, chi tiết khác:
Hoạt động khám phá trang 25 Toán 12 Tập 1: Cho hàm số y = – x2 + 4x – 3. ....
Thực hành 1 trang 28 Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: ....
Thực hành 2 trang 30 Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: ....
Thực hành 3 trang 32 Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: ....