Bài 7 trang 18 Toán 12 Tập 1 Chân trời sáng tạo

Hộp sữa 1 l được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.

Giải Toán 12 Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số - Chân trời sáng tạo

Bài 7 trang 18 Toán 12 Tập 1: Hộp sữa 1 l được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.

Lời giải:

Gọi chiều cao của hộp sữa là h (cm), h > 0.

Theo đề ta có V = 1 lít = 1000 cm³ = x².h $\iff h=\frac{1000}{x^2}$.

Diện tích toàn phần của hộp sữa là S(x) = 2x² + 4xh = $2x^2+\frac{4000}{x}$.

Bài toán trở thành tìm giá trị nhỏ nhất của hàm số S(x) khi x > 0.

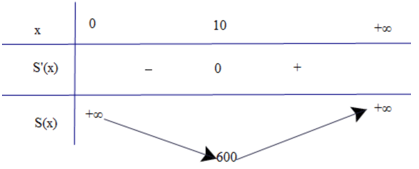
Có S'(x) = $4x-\frac{4000}{x^2}$; S'(x) = 0 ⇔ x = 10.

Bảng biến thiên

Vậy diện tích toàn phần của hộp nhỏ nhất khi x = 10 cm.

Lời giải bài tập Toán 12 Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số hay, chi tiết khác:

• Hoạt động khởi động trang 14 Toán 12 Tập 1: Sự phân hủy của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hòa tan trong nước ....

• Hoạt động khám phá 1 trang 14 Toán 12 Tập 1: Hình 1 cho biết sự thay đổi của nhiệt độ ở một thành phố trong một ngày ....

• Thực hành 1 trang 16 Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: ....

• Vận dụng trang 16 Toán 12 Tập 1: Sử dụng đạo hàm và lập bảng biến thiên, trả lời câu hỏi trong mục khởi động (trang 14). ....

• Hoạt động khám phá 2 trang 16 Toán 12 Tập 1: Hình 3 cho ta đồ thị của ba hàm số ....

• Thực hành 2 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $g\left(x\right)=x+\frac{4}{x^2}$ trên đoạn [1; 4] ....

• Thực hành 3 trang 18 Toán 12 Tập 1: Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu? ....

• Bài 1 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5 ....

• Bài 2 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau ....

• Bài 3 trang 18 Toán 12 Tập 1: Tìm giá trị nhỏ nhất của các hàm số sau ....

• Bài 4 trang 18 Toán 12 Tập 1: Khi làm nhà kho, bác An muốn cửa số có dạng hình chữ nhật với chu vi bằng 4 m (Hình 6) ....

• Bài 5 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=2\sqrt{1-x^2}+x^2$. ....

• Bài 6 trang 18 Toán 12 Tập 1: Khối lượng q (kg) của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc ....