Giải Toán 12 trang 34 Tập 2 Chân trời sáng tạo

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 34 Tập 2 trong Bài 1: Phương trình mặt phẳng Toán 12 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 34.

Giải Toán 12 trang 34 Tập 2 Chân trời sáng tạo

Thực hành 2 trang 34 Toán 12 Tập 2: Cho mặt phẳng (Q) đi qua ba điểm A(1; 1; 1), B(−1; 1; 5), C(10; 7; −1). Tìm cặp vectơ chỉ phương và một vectơ pháp tuyến của (Q).

Lời giải:

Ta có $\overrightarrow{AB}=\left(-2;0;4\right),\overrightarrow{AC}=\left(9;6;-2\right)$ là cặp vectơ chỉ phương của mặt phẳng (Q).

Có $\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(\left|\begin{array}{cc}0& 4\\ 6& -2\end{array}\right|;\left|\begin{array}{cc}4& -2\\ -2& 9\end{array}\right|;\left|\begin{array}{cc}-2& 0\\ 9& 6\end{array}\right|\right)$ = $\left(-24;32;-12\right)$

Do đó mặt phẳng (Q) nhận $\overrightarrow{n}=\frac{1}{4}\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(-6;8;-3\right)$ làm một vectơ pháp tuyến.

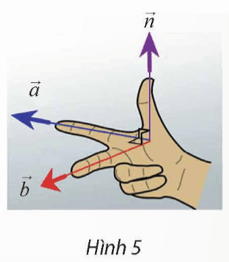
Vận dụng 2 trang 34 Toán 12 Tập 2: Cho biết hai vectơ $\overrightarrow{a}=\left(2;1;1\right)$, $\overrightarrow{b}=\left(1;-2;0\right)$ có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong Hình 5. Tìm vectơ $\overrightarrow{n}$ có giá song song với ngón cái. (Xem như ba ngón tay nói trên tạo thành ba đường thẳng đôi một vuông góc).

Lời giải:

Ta có $\left[\overrightarrow{a},\overrightarrow{b}\right]=\left(\left|\begin{array}{cc}1& 1\\ -2& 0\end{array}\right|;\left|\begin{array}{cc}1& 2\\ 0& 1\end{array}\right|;\left|\begin{array}{cc}2& 1\\ 1& -2\end{array}\right|\right)=\left(2;1;-5\right)$.

Vậy $\overrightarrow{n}=\left[\overrightarrow{a},\overrightarrow{b}\right]=\left(2;1;-5\right)$ có giá song song với ngón cái.

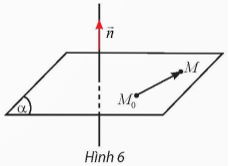
Hoạt động khám phá 3 trang 35 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M₀(1; 2; 3) và nhận $\overrightarrow{n}=\left(7;5;2\right)$ làm vectơ pháp tuyến. Gọi M(x; y; z) là một điểm tùy ý trong không gian. Tính tích vô hướng $\overrightarrow{n}.\overrightarrow{M_{0}M}$ theo x, y, z.

Lời giải:

Ta có $\overrightarrow{M_{0}M}=\left(x-1;y-2;z-3\right)$.

Có $\overrightarrow{n}.\overrightarrow{M_{0}M}=7\left(x-1\right)+5\left(y-2\right)+2\left(z-3\right)$ = 7x + 5y + 2z – 23.

Lời giải bài tập Toán 12 Bài 1: Phương trình mặt phẳng hay khác:

• Giải Toán 12 trang 32
• Giải Toán 12 trang 33
• Giải Toán 12 trang 36
• Giải Toán 12 trang 38
• Giải Toán 12 trang 40
• Giải Toán 12 trang 42
• Giải Toán 12 trang 43