Giải Toán 12 trang 62 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 12 trang 62 Tập 1 trong Bài 3: Biểu thức toạ độ của các phép toán vectơ Toán 12 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 62.

Giải Toán 12 trang 62 Tập 1 Chân trời sáng tạo

Thực hành 4 trang 62 Toán 12 Tập 1: Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(−3;−1; 0). Tìm tọa độ:

a) Các điểm M', N', P' lần lượt là trung điểm của các cạnh NP, MP, MN;

b) Trọng tâm G của tam giác M'N'P'.

Lời giải:

a) Tọa độ trung điểm M' của cạnh NP là

$M^{\text{'}}\left(\frac{1-3}{2};\frac{2-1}{2};\frac{3+0}{2}\right)$ hay $M^{\text{'}}\left(-1;\frac{1}{2};\frac{3}{2}\right)$ .

Tọa độ trung điểm N' của cạnh MP là

$N^{\text{'}}\left(\frac{2-3}{2};\frac{1-1}{2};\frac{3+0}{2}\right)$ hay $N^{\text{'}}\left(\frac{-1}{2};0;\frac{3}{2}\right)$ .

Tọa độ trung điểm P' của cạnh MN là

$P^{\text{'}}\left(\frac{2+1}{2};\frac{1+2}{2};\frac{3+3}{2}\right)$ hay $P^{\text{'}}\left(\frac{3}{2};\frac{3}{2};3\right)$ .

b) Tọa độ trọng tâm G là:

$G\left(\frac{-1-\frac{1}{2}+\frac{3}{2}}{3};\frac{\frac{1}{2}+0+\frac{3}{2}}{3};\frac{\frac{3}{2}+\frac{3}{2}+3}{3}\right)$ hay $G\left(0;\frac{2}{3};2\right)$ .

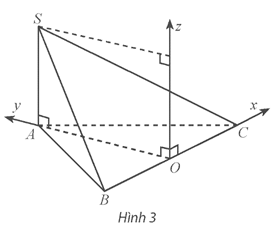
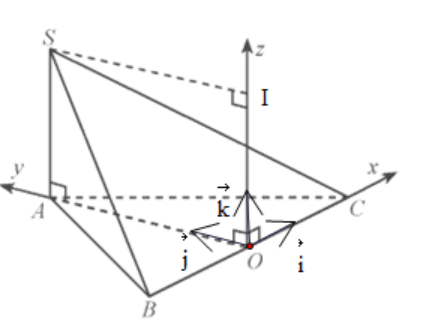
Vận dụng 3 trang 62 Toán 12 Tập 1: Cho hình chóp S.ABC có SA $\perp$ (ABC), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ tọa độ như Hình 3, hãy tìm tọa độ:

a) Các điểm A, S, B, C.

b) Trung điểm M của SB và trung điểm N của SC.

c) Trọng tâm G của tam giác SBC.

Lời giải:

a)

Vì ABC là tam giác đều cạnh a, O là trung điểm của BC nên AO là đường cao.

Suy ra $AO=a\frac{\sqrt{3}}{2}$ và OB = OC = $\frac{a}{2}$ .

Vì $\overrightarrow{OC}$ và $\overrightarrow{i}$ cùng hướng và $OC=\frac{a}{2}$ nên $\overrightarrow{OC}=\frac{a}{2}\overrightarrow{i}$ . Suy ra $C\left(\frac{a}{2};0;0\right)$ .

Vì $\overrightarrow{OB}$ và $\overrightarrow{i}$ ngược hướng và $OB=\frac{a}{2}$ nên $\overrightarrow{OB}=-\frac{a}{2}\overrightarrow{i}$ . Suy ra $B\left(-\frac{a}{2};0;0\right)$ .

Vì $\overrightarrow{OA}$ và $\overrightarrow{j}$ cùng hướng và $OA=\frac{a\sqrt{3}}{2}$ nên $\overrightarrow{OA}=\frac{a\sqrt{3}}{2}\overrightarrow{j}$ . Suy ra $A\left(0;\frac{a\sqrt{3}}{2};0\right)$

Gọi I là hình chiếu của S trên Oz.

Ta có OI = SA.

Vì OI và $\overrightarrow{k}$ cùng hướng và OI = a nên $\overrightarrow{OI}=a\overrightarrow{k}$ .

Theo quy tắc hình bình hành có: $\overrightarrow{OS}=\overrightarrow{OA}+\overrightarrow{OI}=\frac{a\sqrt{3}}{2}\overrightarrow{j}+a\overrightarrow{k}$ .

Do đó $S\left(0;\frac{a\sqrt{3}}{2};a\right)$ .

b) Tọa độ trung điểm M của SB là

$M\left(\frac{0-\frac{a}{2}}{2};\frac{\frac{a\sqrt{3}}{2}+0}{2};\frac{a+0}{2}\right)$ hay $M\left(-\frac{a}{4};\frac{a\sqrt{3}}{4};\frac{a}{2}\right)$ .

Tọa độ trung điểm N của SC là

$N\left(\frac{0+\frac{a}{2}}{2};\frac{\frac{a\sqrt{3}}{2}+0}{2};\frac{a+0}{2}\right)$ hay $N\left(\frac{a}{4};\frac{a\sqrt{3}}{4};\frac{a}{2}\right)$ .

c) Tọa độ trọng tâm G của tam giác SBC là:

$G\left(\frac{0-\frac{a}{2}+\frac{a}{2}}{3};\frac{0+\frac{a\sqrt{3}}{2}+0}{3};\frac{0+a+0}{3}\right)$ hay $G\left(0;\frac{a\sqrt{3}}{6};\frac{a}{3}\right)$ .

Lời giải bài tập Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ hay khác:

• Giải Toán 12 trang 58

• Giải Toán 12 trang 59

• Giải Toán 12 trang 60

• Giải Toán 12 trang 61

• Giải Toán 12 trang 64