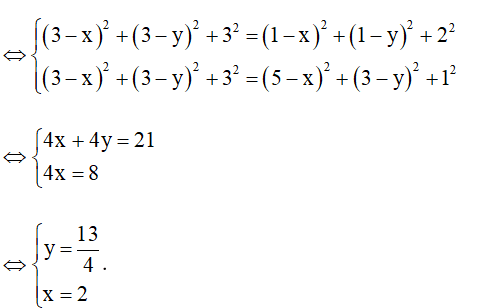Giải Toán 12 trang 64 Tập 1 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

Với Giải Toán 12 trang 64 Tập 1 trong Bài 3: Biểu thức toạ độ của các phép toán vectơ Toán 12 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 64.

Giải Toán 12 trang 64 Tập 1 Chân trời sáng tạo

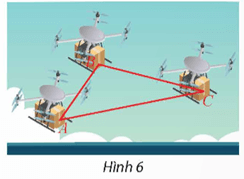
Vận dụng 4 trang 64 Toán 12 Tập 1: Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có tọa độ là A(1; 1; 1), B(5; 7; 9), C(9; 11; 4). Tính:

a) Các khoảng cách giữa mỗi cặp drone giao hàng.

b) Góc $\hat{B A C}$ .

Vận dụng 4 trang 64 Toán 12 Tập 1 Chân trời sáng tạo

Lời giải:

a) Ta có $\vec{A B} = (4; 6; 8)$ ; $\vec{A C} = (8; 10; 3)$ ; $\vec{B C} = (4; 4; - 5)$ .

Khi đó: $|\vec{A B}| = \sqrt{4^{2} + 6^{2} + 8^{2}} = 2 \sqrt{29}$ ;

$|\vec{A C}| = \sqrt{8^{2} + 10^{2} + 3^{2}} = \sqrt{173}$ ;

$\vec{B C} = \sqrt{4^{2} + 4^{2} + {(- 5)}^{2}} = \sqrt{57}$ .

b) Ta có $\cos \hat{B A C} = \frac{\vec{A B} . \vec{A C}}{|\vec{A B}| . |\vec{A C}|} = \frac{4.8 + 6.10 + 8.3}{2 \sqrt{29} . \sqrt{173}} = \frac{119}{2 \sqrt{5017}}$ $\Rightarrow \hat{B A C} \approx 35 ° 2'$ .

Bài 1 trang 64 Toán 12 Tập 1: Tính:

a) $\vec{a} . \vec{b}$ với $\vec{a} = (5; 2; - 4), \vec{b} = (4; - 2; 2)$ .

b) $\vec{c} . \vec{d}$ với $\vec{c} = (2; - 3; 4), \vec{d} = (6; 5; - 3)$ .

Lời giải:

a) $\vec{a} . \vec{b} = 5.4 + 2. (- 2) + (- 4) .2 = 8$ .

b) $\vec{c} . \vec{d} = 2.6 + (- 3) .5 + 4. (- 3) = - 15$ .

Bài 2 trang 64 Toán 12 Tập 1: Cho hai vectơ $\vec{a} = (0; 1; 3)$ và $\vec{b} = (- 2; 3; 1)$ . Tìm tọa độ của vectơ $2 \vec{b} - \frac{3}{2} \vec{a}$ .

Lời giải:

Có $\frac{3}{2} \vec{a} = (0; \frac{3}{2}; \frac{9}{2})$ ; $2 \vec{b} = (- 4; 6; 2)$ .

Tọa độ của vectơ $2 \vec{b} - \frac{3}{2} \vec{a}$ là $(- 4 - 0; 6 - \frac{3}{2}; 2 - \frac{9}{2})$ hay $(- 4; \frac{9}{2}; - \frac{5}{2})$ .

Bài 3 trang 64 Toán 12 Tập 1: Cho ba điểm A(2; 1; −1), B(3; 2; 0) và C(2; −1; 3).

a) Chứng minh A, B, C là ba đỉnh của một tam giác. Tính chu vi tam giác ABC.

b) Tìm tọa độ trung điểm của các cạnh của tam giác ABC.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

Lời giải:

a) Ta có $\vec{A B} = (1; 1; 1), \vec{A C} = (0; - 2; 4), \vec{B C} = (- 1; - 3; 3)$ .

Vì $\vec{A B}$ và $\vec{A C}$ không cùng phương nên A, B, C không thẳng hàng.

Do đó A, B, C là ba đỉnh của một tam giác.

Ta có chu vi tam giác ABC là:

AB + AC + BC

= $\sqrt{1^{2} + 1^{2} + 1^{2}} + \sqrt{0^{2} + {(- 2)}^{2} + 4^{2}} + \sqrt{{(- 1)}^{2} + {(- 3)}^{2} + 3^{2}}$

$= \sqrt{3} + 2 \sqrt{5} + \sqrt{19}$

b) Gọi M, N, P lần lượt là trung điểm của cạnh AB, BC, CA.

Tọa độ điểm M là

$M (\frac{2 + 3}{2}; \frac{1 + 2}{2}; \frac{- 1 + 0}{2})$ hay $M (\frac{5}{2}; \frac{3}{2}; \frac{- 1}{2})$ .

Tọa độ điểm N là

$N (\frac{3 + 2}{2}; \frac{2 - 1}{2}; \frac{0 + 3}{2})$ hay $N (\frac{5}{2}; \frac{1}{2}; \frac{3}{2})$ .

Tọa độ điểm P là

$P (\frac{2 + 2}{2}; \frac{1 - 1}{2}; \frac{- 1 + 3}{2})$ hay $P (2; 0; 1)$ .

c) Tọa độ trọng tâm G của tam giác ABC là

$G (\frac{2 + 3 + 2}{3}; \frac{1 + 2 - 1}{3}; \frac{- 1 + 0 + 3}{3})$ hay $G (\frac{7}{3}; \frac{2}{3}; \frac{2}{3})$ .

Bài 4 trang 64 Toán 12 Tập 1: Cho điểm M(1; 2; 3). Hãy tìm tọa độ của các điểm:

a) M₁, M₂, M₃ lần lượt là hình chiếu vuông góc của M trên các mặt phẳng (Oxy), (Oyz), (Oxz).

b) Gọi M', M", M"' lần lượt là các điểm thỏa mãn:

• O là trung điểm của MM';

• MM" vuông góc với mặt phẳng (Oxy) tại điểm H sao cho H là trung điểm của MM".

• MM"' vuông góc và cắt trục Oy tại điểm K sao cho K là trung điểm của MM"'.

Lời giải:

a) Ta có M₁(1; 2; 0), M₂(0; 2; 3), M₃(1; 0; 3).

b) +) Vì O là trung điểm của MM' nên

$\{\begin{cases} x_{M^{'}} = 2 x_{O} - x_{M} \\ y_{M^{'}} = 2 y_{O} - y_{M} \\ z_{M^{'}} = 2 z_{O} - z_{M} \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{M^{'}} = 2.0 - 1 \\ y_{M^{'}} = 2.0 - 2 \\ z_{M^{'}} = 2.0 - 3 \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{M^{'}} = - 1 \\ y_{M^{'}} = - 2 \\ z_{M^{'}} = - 3 \end{cases}$

Vậy M'(−1; −2; −3).

+) Vì H $\in$ (Oxy) nên H(x; y; 0).

Ta có $\vec{M H} = (x - 1; y - 2; - 3)$ .

Vì MH $⊥$ (Oxy) $\Rightarrow \{\begin{cases} M H ⊥ O x \\ M H ⊥ O y \end{cases}$ $\Rightarrow \{\begin{cases} \vec{M H} . \vec{i} = 0 \\ \vec{M H} . \vec{j} = 0 \end{cases}$ $\Rightarrow \{\begin{cases} x - 1 = 0 \\ y - 2 = 0 \end{cases}$ $\Rightarrow \{\begin{cases} x = 1 \\ y = 2 \end{cases}$

Do đó H(1; 2; 0).

Vì H là trung điểm của MM" nên

$\{\begin{cases} x_{M^{''}} = 2 x_{H} - x_{M} \\ y_{M^{''}} = 2 y_{H} - y_{M} \\ z_{M^{''}} = 2 z_{H} - z_{M} \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{M^{''}} = 2.1 - 1 \\ y_{M^{''}} = 2.2 - 2 \\ z_{M^{''}} = 2.0 - 3 \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{M^{''}} = 1 \\ y_{M^{''}} = 2 \\ z_{M^{''}} = - 3 \end{cases}$

Vậy M"(1; 2; −3).

+) Vì K $\in$ Oy nên K(0; y; 0) $\Rightarrow \vec{M K} = (- 1; y - 2; - 3)$

Vì $M K ⊥ O y$ nên $\vec{H K} . \vec{j} = 0$ $\Leftrightarrow y - 2 = 0 \Leftrightarrow y = 2$ . Do đó K(0; 2; 0).

Vì K là trung điểm của MM"' nên

$\{\begin{cases} x_{{M^{''}}^{'}} = 2 x_{K} - x_{M} \\ y_{{M^{''}}^{'}} = 2 y_{K} - y_{M} \\ z_{{M^{''}}^{'}} = 2 z_{K} - z_{M} \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{{M^{''}}^{'}} = 2.0 - 1 \\ y_{{M^{''}}^{'}} = 2.2 - 2 \\ z_{{M^{''}}^{'}} = 2.0 - 3 \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{{M^{''}}^{'}} = - 1 \\ y_{{M^{''}}^{'}} = 2 \\ z_{{M^{''}}^{'}} = - 3 \end{cases}$

Vậy M'''(−1; 2; −3).

Bài 5 trang 64 Toán 12 Tập 1: Cho ba điểm A(3; 3; 3), B(1; 1; 2) và C(5; 3; 1).

a) Tìm điểm M trên trục Oy cách đều hai điểm B, C.

b) Tìm điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C.

Lời giải:

a) Vì M $\in$ Oy nên M(0; y; 0).

Vì M cách đều hai điểm B, C nên MB = MC hay MB² = MC²

$\Leftrightarrow 1^{2} + {(1 - y)}^{2} + 2^{2} = 5^{2} + {(3 - y)}^{2} + 1^{2}$

$\Leftrightarrow 4 y = 29 \Leftrightarrow y = \frac{29}{4}$

Vậy $M (0; \frac{29}{4}; 0)$ .

b) Vì N $\in$ (Oxy) nên N(x; y; 0).

Vì N cách đều ba điểm A, B, C nên NA = NB = NC hay NA² = NB² = NC²

Bài 5 trang 64 Toán 12 Tập 1 Chân trời sáng tạo

Vậy $N (2; \frac{13}{4}; 0)$ .

Bài 6 trang 64 Toán 12 Tập 1: Cho các điểm A(−1; −1; 0), B(0; 3; −1), C(−1; 14; 0), D(−3; 6; 2). Chứng minh rằng ABCD là hình thang.

Ta có $\vec{A B} = (1; 4; - 1)$ , $\vec{A C} = (0; 15; 0)$ , $\vec{D C} = (2; 8; - 2)$ .

Vì $\vec{D C} = (2; 8; - 2) = 2 (1; 4; - 1) = 2 \vec{A B}$ nên $\vec{D C}$ và $\vec{A B}$ cùng phương.

Mặt khác $\vec{A B}$ và $\vec{A C}$ không cùng phương nên CD // AB.

Do đó ABCD là hình thang.

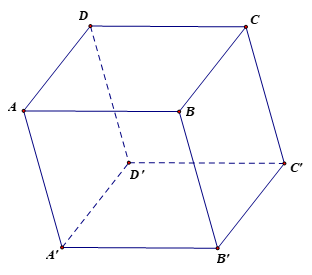
Bài 7 trang 64 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D' có A(1; 0; 1), B(2; 1; 2), D(1; −1; 1), C'(4; 5; −5). Tìm tọa độ các đỉnh còn lại của hình hộp.

Bài 7 trang 64 Toán 12 Tập 1 Chân trời sáng tạo

Do ABCD.A'B'C'D' là hình hộp nên các mặt là hình bình hành.

Ta có $\vec{A D} = \vec{B C}$ $\Leftrightarrow \{\begin{cases} 1 - 1 = x_{C} - 2 \\ - 1 - 0 = y_{C} - 1 \\ 1 - 1 = z_{C} - 2 \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{C} = 2 \\ y_{C} = 0 \\ z_{C} = 2 \end{cases}$ .

Vậy C(2; 0; 2).

Ta có $\vec{D C} = \vec{D^{'} C^{'}}$ $\Leftrightarrow \{\begin{cases} 2 - 1 = 4 - x_{D^{'}} \\ 1 = 5 - y_{D^{'}} \\ 2 - 1 = - 5 - z_{D^{'}} \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{D^{'}} = 3 \\ y_{D^{'}} = 4 \\ z_{D^{'}} = - 6 \end{cases}$ .

Vậy D'(3; 4; −6).

Ta có $\vec{A D} = \vec{A^{'} D^{'}}$ $\Leftrightarrow \{\begin{cases} 1 - 1 = 3 - x_{A^{'}} \\ - 1 - 0 = 4 - y_{A^{'}} \\ 1 - 1 = - 6 - z_{A^{'}} \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{A^{'}} = 3 \\ y_{A^{'}} = 5 \\ z_{A^{'}} = - 6 \end{cases}$ .

Vậy A'(3; 5; −6).

Ta có $\vec{A^{'} D^{'}} = \vec{B^{'} C^{'}}$ $\Leftrightarrow \{\begin{cases} 3 - 3 = 4 - x_{B^{'}} \\ 4 - 5 = 5 - y_{B^{'}} \\ - 6 + 6 = - 5 - z_{B^{'}} \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{B^{'}} = 4 \\ y_{B^{'}} = 6 \\ z_{B^{'}} = - 5 \end{cases}$ .

Vậy B'(4; 6; −5).

Bài 8 trang 64 Toán 12 Tập 1: Tính công sinh bởi lực $\vec{F} (20; 30; - 10)$ (đơn vị: N) tạo bởi một drone giao hàng (Hình 7) khi thực hiện một độ dịch chuyển $\vec{d} = (150; 200; 100)$ (đơn vị: m).

Lời giải:

Bài 8 trang 64 Toán 12 Tập 1 Chân trời sáng tạo

Lời giải:

Công sinh bởi lực $\vec{F}$ là $A = \vec{F} . \vec{d}$ = 20.150 + 30.200 + (-10).100 = 8000 J.

Lời giải bài tập Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ hay khác:

Xem thêm lời giải bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯