Giải Toán 12 trang 39 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 39 Tập 2 trong Bài 14: Phương trình mặt phẳng Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 39.

Giải Toán 12 trang 39 Tập 2 Kết nối tri thức

Luyện tập 11 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, cho hai mặt phẳng (P): x + 3y + z + 2 = 0 và (Q): x + 3y + z + 5 = 0.

a) Chứng minh rằng (P) và (Q) song song với nhau.

b) Lấy một điểm thuộc (P), tính khoảng cách từ điểm đó đến (Q). Từ đó tính khoảng cách giữa hai mặt phẳng (P) và (Q).

Lời giải:

a) Ta có $\overrightarrow{n_P}=\left(1;3;1\right),\overrightarrow{n_Q}=\left(1;3;1\right)$

Vì $\overrightarrow{n_P}=\overrightarrow{n_Q}$ và 2 ≠ 5. Do đó (P) và (Q) song song với nhau.

b) Lấy điểm M(0; 0; −2) ∈ (P).

Khi đó khoảng cách từ M đến mặt phẳng (Q) là:

$d\left(M,\left(Q\right)\right)=\frac{\left|-2+5\right|}{\sqrt{1+3^2+1}}=\frac{3}{\sqrt{11}}$

Do đó $d\left(M,\left(Q\right)\right)=d\left(\left(P\right),\left(Q\right)\right)=\frac{3}{\sqrt{11}}$

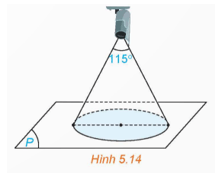
Vận dụng 5 trang 39 Toán 12 Tập 2: (H.5.14) Góc quan sát ngang của một camera là 115°. Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 4) và chiếu thẳng về phía mặt phẳng (P): x + 2y + 2z + 3 = 0. Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có bán kính bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất)

Lời giải:

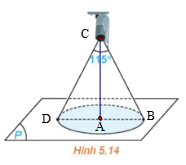
Chọn các điểm như hình vẽ.

Gọi A là hình chiếu của C trên mặt phẳng (P).

Vì CBD là tam giác cân nên CA là đường cao, phân giác, trung tuyến của BD.

Ta có $CA=d\left(C,\left(P\right)\right)=\frac{\left|1+2.2+2.4+3\right|}{\sqrt{1+2^2+2^2}}=\frac{16}{3}$

Vì tam giác CAB vuông tại A, có $\widehat{ACB}=\frac{115°}{2}=\mathrm{57,5}°$

Suy ra R = AB = CA.tan57,5° ≈ 8,4.

Vậy vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có bán kính bằng 8,4.

Bài 5.1 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, viết phương trình mặt phẳng đi qua điểm M(1; 2; −1) và vuông góc với trục Ox.

Lời giải:

Gọi mặt phẳng cần tìm là mặt phẳng (P).

Vì mặt phẳng (P) vuông góc với trục Ox nên nhận $\overrightarrow{i}=\left(1;0;0\right)$ làm một vectơ pháp tuyến.

Mặt phẳng (P) đi qua điểm M(1; 2; −1) và nhận $\overrightarrow{i}=\left(1;0;0\right)$ làm một vectơ pháp tuyến có phương trình là: x – 1 = 0.

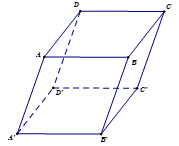
Bài 5.2 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, cho hình hộp ABCD.A'B'C'D', với A(1; −1; 3), B(0; 2; 4), D(2; −1; 1), A'(0; 1; 2).

a) Tìm tọa độ các điểm C, B', D'.

b) Viết phương trình mặt phẳng (CB'D').

Lời giải:

a) Ta có $\overrightarrow{AD}=\left(1;0;-2\right),\overrightarrow{A{A}^{\text{'}}}=\left(-1;2;-1\right),\overrightarrow{AB}=\left(-1;3;1\right)$

Vì ABCD là hình bình hành nên $\overrightarrow{AD}=\overrightarrow{BC}$$\iff \left\{\begin{array}{l}{x}_C=1\\ y_C-2=0\\ z_C-4=-2\end{array}\right.$$\iff \left\{\begin{array}{l}{x}_C=1\\ y_C=2\\ z_C=2\end{array}\right.$

Vậy C(1; 2; 2).

Vì ABB'A' là hình bình hành nên $\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{B{B}^{\text{'}}}$$\iff \left\{\begin{array}{l}{x}_{B^{\text{'}}}=-1\\ y_{B^{\text{'}}}-2=2\\ z_{C^{\text{'}}}-4=-1\end{array}\right.$$\iff \left\{\begin{array}{l}{x}_{B^{\text{'}}}=-1\\ y_{B^{\text{'}}}=4\\ z_{C^{\text{'}}}=3\end{array}\right.$

Vậy B'(−1; 4; 3).

Vì ADD'A' là hình bình hành nên $\overrightarrow{AD}=\overrightarrow{A^{\text{'}}{D}^{\text{'}}}$$\iff \left\{\begin{array}{l}{x}_{D^{\text{'}}}=1\\ y_{D^{\text{'}}}-1=0\\ z_{D^{\text{'}}}-2=-2\end{array}\right.$$\iff \left\{\begin{array}{l}{x}_{D^{\text{'}}}=1\\ y_{D^{\text{'}}}=1\\ z_{D^{\text{'}}}=0\end{array}\right.$

Vậy D'(1; 1; 0).

b) Ta có: $\overrightarrow{C{B}^{\text{'}}}=\left(-2;2;1\right),\overrightarrow{C{D}^{\text{'}}}=\left(0;-1;-2\right)$

Vì mặt phẳng (CB'D') có cặp vectơ chỉ phương là $\overrightarrow{C{B}^{\text{'}}},\overrightarrow{C{D}^{\text{'}}}$ nên có một vectơ pháp tuyến là:

$\overrightarrow{n}=\left[\overrightarrow{C{B}^{\text{'}}},\overrightarrow{C{D}^{\text{'}}}\right]=\left(\left|\begin{array}{cc}2& 1\\ -1& -2\end{array}\right|;\left|\begin{array}{cc}1& -2\\ -2& 0\end{array}\right|;\left|\begin{array}{cc}-2& 2\\ 0& -1\end{array}\right|\right)$ = (−3; −4; 2).

Mặt phẳng (CB'D') đi qua điểm C(1; 2; 2) và nhận $\overrightarrow{n}=\left(-3;-4;2\right)$ là một vectơ pháp tuyến có phương trình là:

−3(x – 1) −4(y – 2) + 2(z −2) = 0 ⇔ 3x + 4y – 2z – 7 = 0.

Bài 5.3 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(1; −1; 5) và vuông góc với hai mặt phẳng (Q): 3x + 2y – z = 0, (R): x + y – z = 0.

Lời giải:

Ta có $\overrightarrow{n_Q}=\left(3;2;-1\right),\overrightarrow{n_R}=\left(1;1;-1\right)$

Vì (P) ^ (Q) và (P) ^ (R) nên $\overrightarrow{n_P}=\left[\overrightarrow{n_Q},\overrightarrow{n_R}\right]=\left(-1;2;1\right)$

Mặt phẳng (P) đi qua điểm M(1; −1; 5) và nhận $\overrightarrow{n_P}=\left(-1;2;1\right)$ làm một vectơ pháp tuyến có phương trình là:

−(x – 1) + 2(y + 1) + (z – 5) = 0 ⇔ x – 2y – z + 2 = 0.

Bài 5.4 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, viết phương trình mặt phẳng đi qua M(2; 3; −1), song song với trục Ox và vuông góc với mặt phẳng (Q): x + 2y – 3z + 1 = 0.

Lời giải:

Gọi mặt phẳng cần tìm là mặt phẳng (P).

Ta có $\overrightarrow{i}=\left(1;0;0\right)$ và $\overrightarrow{n_Q}=\left(1;2;-3\right)$

Vì (P) // Ox và (P) ⊥ (Q) nên $\overrightarrow{n_P}=\left[\overrightarrow{i},\overrightarrow{n_Q}\right]=\left(0;3;2\right)$

Mặt phẳng đi qua M(2; 3; −1) và nhận $\overrightarrow{n_P}=\left(0;3;2\right)$ làm một vectơ pháp tuyến có phương trình là: 3(y – 3) + 2(z + 1) = 0 ⇔ 3y + 2z – 7 = 0.

Bài 5.5 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, tính khoảng cách từ gốc tọa độ đến mặt phẳng (P): 2x + 2y – z + 1 = 0.

Lời giải:

Ta có O(0; 0; 0).

Ta có $d\left(O,\left(P\right)\right)=\frac{\left|1\right|}{\sqrt{2^2+2^2+{\left(-1\right)}^2}}=\frac{1}{3}$

Bài 5.6 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, cho hai mặt phẳng (P): x + y + z + 2 = 0, (Q): x + y + z + 6 = 0. Chứng minh rằng hai mặt phẳng đã cho song song với nhau và tính khoảng cách giữa hai mặt phẳng đó.

Lời giải:

Vì $\overrightarrow{n_P}=\overrightarrow{n_Q}=\left(1;1;1\right)$ và 2 ≠ 6 nên (P) // (Q).

Lấy M(0; 0; −2) ∈ (P).

Khi đó $d\left(M,\left(Q\right)\right)=d\left(\left(P\right),\left(Q\right)\right)=\frac{\left|-2+6\right|}{\sqrt{1+1+1}}=\frac{4}{\sqrt{3}}$

Bài 5.7 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, cho hai mặt phẳng (P): x + 3y – z = 0, (Q): x – y – 2z + 1 = 0.

a) Chứng minh rằng hai mặt phẳng (P) và (Q) vuông góc với nhau.

b) Tìm điểm M thuộc trục Ox và cách đều hai mặt phẳng (P) và (Q).

Lời giải:

a) Ta có $\overrightarrow{n_P}=\left(1;3;-1\right),\overrightarrow{n_Q}=\left(1;-1;-2\right)$

Vì $\overrightarrow{n_P}.\overrightarrow{n_Q}=1.1+3.\left(-1\right)+\left(-1\right).\left(-2\right)=0$

Do đó hai mặt phẳng (P) và (Q) vuông góc với nhau.

b) Vì M Î Ox nên M(a; 0; 0).

Vì d(M, (P)) = d(M, (Q)) nên $\frac{\left|a\right|}{\sqrt{1+9+1}}=\frac{\left|a+1\right|}{\sqrt{1+1+4}}$$\iff \sqrt{6}\left|a\right|=\sqrt{11}\left|a+1\right|$

$\iff 6a^2=11a^2+22a+11$$\iff 5a^2+22a+11=0$$\iff a=\frac{-11-\sqrt{66}}{5}$ hoặc $a=\frac{-11+\sqrt{66}}{5}$

Vậy có hai điểm M thỏa mãn yêu cầu là:

$M_1\left(\frac{-11-\sqrt{66}}{5};0;0\right),M_2\left(\frac{-11+\sqrt{66}}{5};0;0\right)$

Bài 5.8 trang 39 Toán 12 Tập 2: Bác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều và các mái nhà kề nhau thì vuông góc với nhau. Hỏi ý tưởng trên có thực hiện được không?

Lời giải:

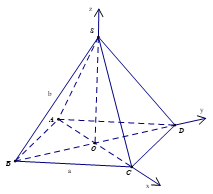
Giả sử mái nhà của ngôi nhà được minh họa như hình vẽ trên.

Ta gắn hệ trục tọa độ như hình vẽ.

Gọi các cạnh đáy của hình chóp có độ dài là a, các cạnh bên có độ dài là b.

Vì ABCD là hình vuông cạnh a nên $OA=OB=OC=OD=\frac{AC}{2}=\frac{a\sqrt{2}}{2}$

Vì SO là đường cao của tam giác SOC nên $SO=\sqrt{S{C}^2-O{C}^2}=\sqrt{b^2-\frac{a^2}{2}}=\sqrt{\frac{2b^2-a^2}{2}}.$

Khi đó, ta có: O(0; 0; 0), $A\left(-\frac{a\sqrt{2}}{2};0;0\right),C\left(\frac{a\sqrt{2}}{2};0;0\right),B\left(0;-\frac{a\sqrt{2}}{2};0\right),D\left(0;\frac{a\sqrt{2}}{2};0\right)$ và $S\left(0;0;\sqrt{\frac{2b^2-a^2}{2}}\right)$

Ta có $\overrightarrow{SC}=\left(\frac{a\sqrt{2}}{2};0;-\sqrt{\frac{2b^2-a^2}{2}}\right)$, $\overrightarrow{DC}=\left(\frac{a\sqrt{2}}{2};-\frac{a\sqrt{2}}{2};0\right)$, $\overrightarrow{BC}=\left(\frac{a\sqrt{2}}{2};\frac{a\sqrt{2}}{2};0\right)$

Có $\left[\overrightarrow{SC},\frac{\sqrt{2}}{a}\overrightarrow{DC}\right]=$$\left(\left|\begin{array}{cc}0& -\sqrt{\frac{2b^2-a^2}{2}}\\ -1& 0\end{array}\right|;\left|\begin{array}{cc}-\sqrt{\frac{2b^2-a^2}{2}}& \frac{a\sqrt{2}}{2}\\ 0& 1\end{array}\right|;\left|\begin{array}{cc}\frac{a\sqrt{2}}{2}& 0\\ 1& -1\end{array}\right|\right)$

$=\left(-\sqrt{\frac{2b^2-a^2}{2}};-\sqrt{\frac{2b^2-a^2}{2}};-\frac{a\sqrt{2}}{2}\right)$

$\left[\overrightarrow{SC},\frac{\sqrt{2}}{a}\overrightarrow{BC}\right]$

$=\left(\left|\begin{array}{cc}0& -\sqrt{\frac{2b^2-a^2}{2}}\\ 1& 0\end{array}\right|;\left|\begin{array}{cc}-\sqrt{\frac{2b^2-a^2}{2}}& \frac{a\sqrt{2}}{2}\\ 0& 1\end{array}\right|;\left|\begin{array}{cc}\frac{a\sqrt{2}}{2}& 0\\ 1& 1\end{array}\right|\right)$

$=\left(\sqrt{\frac{2b^2-a^2}{2}};-\sqrt{\frac{2b^2-a^2}{2}};\frac{a\sqrt{2}}{2}\right)$

Ta có mặt phẳng (SCD) nhận $\overrightarrow{n_1}=\left[\overrightarrow{SC},\frac{\sqrt{2}}{a}\overrightarrow{DC}\right]$ làm một vectơ pháp tuyến.

Mặt phẳng (SCB) nhận $\overrightarrow{n_2}=\left[\overrightarrow{SC},\frac{\sqrt{2}}{a}\overrightarrow{BC}\right]$ làm một vectơ pháp tuyến.

Vì $\overrightarrow{n_1}.\overrightarrow{n_2}=-\left(\frac{2b^2-a^2}{2}\right)+\left(\frac{2b^2-a^2}{2}\right)-\frac{a^2}{2}=-\frac{a^2}{2}\ne 0$

Do đó hai mặt phẳng (SCD) và (SCB) không vuông góc với nhau.

Do đó ý tưởng trên không thực hiện được.

Bài 5.9 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, một ngôi nhà có sàn nhà thuộc mặt phẳng Oxy, trần nhà tầng 1 thuộc mặt phẳng z – 1 = 0, mái nhà tầng 2 thuộc mặt phẳng x + y + 50z – 100 = 0. Hỏi trong ba mặt phẳng tương ứng chứa sàn nhà, trần tầng 1, mái tầng 2, hai mặt phẳng nào song song với nhau.

Lời giải:

Vì mặt phẳng Oxy vuông góc với Oz nên mặt phẳng Oxy nhận $\overrightarrow{k}=\left(0;0;1\right)$ làm một vectơ pháp tuyến.

Vì mặt phẳng Oxy đi qua điểm O(0; 0; 0) và có vectơ pháp tuyến $\overrightarrow{k}=\left(0;0;1\right)$ nên có phương trình là: z – 0 = 0 hay z = 0.

Mặt phẳng z – 1 = 0 có $\overrightarrow{n_1}=\left(0;0;1\right)$

Vì $\overrightarrow{n_1}=\overrightarrow{k}$ và 0 ≠ −1 nên mặt phẳng chứa sàn nhà song song với trần tầng 1.

Lời giải bài tập Toán 12 Bài 14: Phương trình mặt phẳng hay khác:

• Giải Toán 12 trang 29
• Giải Toán 12 trang 30
• Giải Toán 12 trang 31
• Giải Toán 12 trang 32
• Giải Toán 12 trang 33
• Giải Toán 12 trang 34
• Giải Toán 12 trang 35
• Giải Toán 12 trang 36
• Giải Toán 12 trang 37