Bài 3 trang 96 Toán 7 Tập 2 Cánh diều

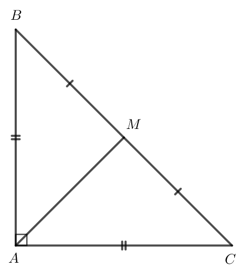
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân.

Giải Toán 7 Bài 7: Tam giác cân - Cánh diều

Bài 3 trang 96 Toán lớp 7 Tập 2: Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân.

Lời giải:

Xét ∆AMB và ∆AMC có:

AM chung.

BM = CM (M là trung điểm của BC).

AB = AC (tam giác ABC cân tại A).

Suy ra ∆AMB = ∆AMC (c - c - c).

Do đó $\hat{M A B} = \hat{M A C}$ (2 góc tương ứng).

Mà $\hat{M A B} + \hat{M A C} = 90 °$ nên $\hat{M A B} = \hat{M A C} = 45 °$ .

Tam giác ABC vuông cân tại A nên $\hat{A B C} = \hat{A C B}$ và $\hat{A B C} + \hat{A C B} = 90 °$ .

Suy ra $\hat{A B C} = \hat{A C B} = 45 °$ .

Tam giác MAB có $\hat{M B A} = \hat{M A B} = 45 °$ nên tam giác MAB cân tại M (1).

Xét tam giác MAB có: $\hat{A M B} = 180 ° - \hat{M B A} - \hat{M A B}$ = 180° - 45° - 45° = 90°.

Suy ra AM ⊥ BM hay tam giác MAB vuông tại M (2).

Từ (1) và (2) suy ra tam giác MAB vuông cân tại M.

Vậy tam giác MAB vuông cân tại M.

Lời giải bài tập Toán 7 Bài 7: Tam giác cân hay, chi tiết khác: