Bài 4 trang 96 Toán 7 Tập 2 Cánh diều

Giải Toán 7 Bài 7: Tam giác cân - Cánh diều

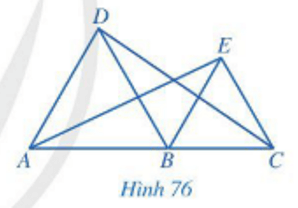
Bài 4 trang 96 Toán lớp 7 Tập 2: Trong Hình 76, cho biết các tam giác ABD và BCE là các tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:

a) AD // BE và BD // CE;

b) $\hat{A B E} = \hat{D B C} = 120 °;$

c) AE = CD.

Lời giải:

a) Tam giác ABD đều nên AB = BD = DA và $\hat{A B D} = \hat{A D B} = \hat{D A B} = 60 °$ .

Tam giác BCE đều nên BC = CE = EB và $\hat{B C E} = \hat{B E C} = \hat{E B C} = 60 °$ .

Ta có $\hat{D A B} = \hat{E B C} (= 60 °)$ , mà 2 góc này ở vị trí đồng vị nên AD // BE.

$\hat{A B D} = \hat{B C E} (= 60 °)$ , mà 2 góc này ở vị trí đồng vị nên BD // CE.

b) $\hat{A B E}$ là góc ngoài tại đỉnh B của ∆EBC nên $\hat{A B E} = \hat{B C E} + \hat{B E C}$ = 60° + 60° = 120°.

$\hat{D B C}$ là góc ngoài tại đỉnh B của ∆ABD nên $\hat{D B C} = \hat{D A B} + \hat{A D B}$ = 60° + 60° = 120°.

c) Xét ∆DBC và ∆ABE có:

DB = AB (chứng minh trên).

$\hat{D B C} = \hat{A B E} (= 120 °)$ .

BC = BE (chứng minh trên).

Suy ra ∆DBC = ∆ABE(c - g - c).

Do đó CD = EA (2 cạnh tương ứng).

Vậy AE = CD.

Lời giải bài tập Toán 7 Bài 7: Tam giác cân hay, chi tiết khác: