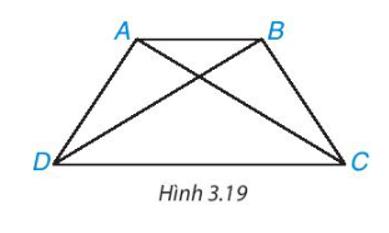
Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh
Câu hỏi:
Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD
Trả lời:
Vì ABCD là hình thang cân (AC // CD) nên AD = BC; .
Xét ∆ACD và ∆BDC có
AD = BC (chứng minh trên);
(chứng minh trên);
Cạnh CD chung.
Do đó ∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).
Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết:
Câu 1:
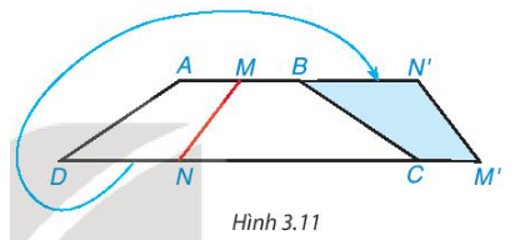
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.
Xem lời giải »
Câu 2:
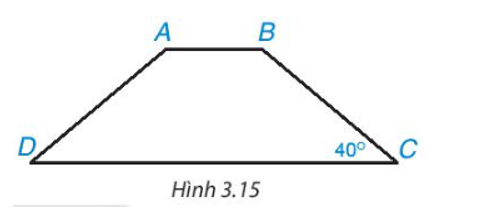
Tính các góc của hình thang cân ABCD (AB // CD), biết (H.3.15).
Xem lời giải »
Câu 3:
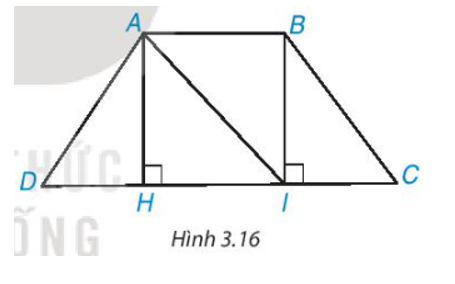
Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
Xem lời giải »
Câu 4:
b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC.
Xem lời giải »
Câu 5:
Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).
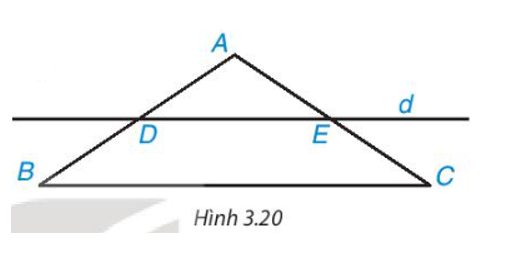
a) Tứ giác DECB là hình gì?
Xem lời giải »
Câu 7:
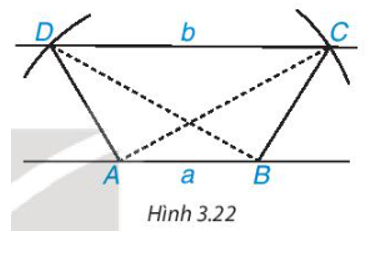
a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau:
- Vẽ hai đường thẳng song song a, b. Trên a lấy hai điểm A, B.
- Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho cung tròn tâm A cắt b tại C; cung tròn tâm B cắt b tại D và hai đoạn thẳng AC, BD cắt nhau. Hình thang ABCD có hai đường chéo AC và BD bằng nhau.
Xem lời giải »
Câu 8:
b) Hình thang ABCD có là hình thang cân không? Vì sao?
Xem lời giải »