Bài 10.14 trang 122 Toán 8 Tập 2 | Kết nối tri thức Giải Toán 8

Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.

Giải Toán 8 Luyện tập chung trang 121, 122 - Kết nối tri thức

Bài 10.14 trang 122 Toán 8 Tập 2: Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.

a) Tính thể tích hình chóp. 

b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31,92 m.

Lời giải:

a) Thể tích hình chóp tứ giác đều là:

V =  $\frac{1}{3}$. S_đáy . h = $\frac{1}{3}$  . 34² . 21 = 8 092 (cm³).

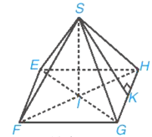
b) Mô tả hình chóp như hình dưới đây.

Ta có SI = 21 m, EF = FG = GH = HE = 34 m, SE = SF = SG = SH = 31,92 m.

SK là một trung đoạn của hình chóp.

K là trung điểm của GH nên GK = KH = $\frac{GH}{2}=\frac{34}{2}=17$  m.

Áp dụng định lí Pythagore cho tam giác SKH vuông tại H, ta có:

KH² + SK² = SH²

Hay 17² + SK² = (31,92)²

Suy ra SK² = (31,92)² – 17² ≈ 729,89. Do đó, SK ≈ 27,02 m.

Diện tích xung quanh của hình chóp tứ giác đều hay tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này là:

S_xq = p . d ≈ $\frac{34\cdot 4}{2}\cdot \mathrm{27,02}$ = 1 837,36 (m²).

Lời giải bài tập Toán 8 Luyện tập chung trang 121, 122 hay, chi tiết khác:

• Bài 10.11 trang 121 Toán 8 Tập 2: Tính thể tích của hình chóp tam giác đều ....

• Bài 10.12 trang 122 Toán 8 Tập 2: Trong các miếng bìa ở Hình 10.32, miếng ....

• Bài 10.13 trang 122 Toán 8 Tập 2: Tính thể tích hình chóp tam giác đều ....