Bài 3.31 trang 72 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.

Giải Toán 8 Bài 14: Hình thoi và hình vuông - Kết nối tri thức

Bài 3.31 trang 72 Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.

Lời giải:

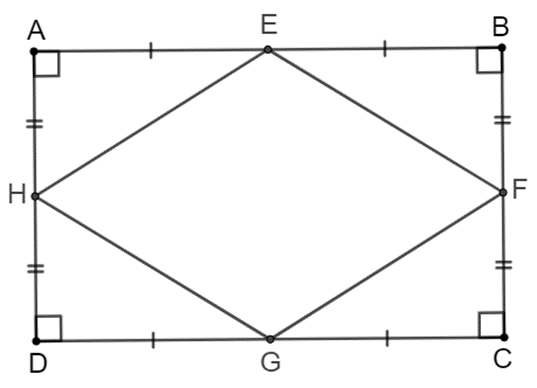
Giả sử có hình chữ nhật ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.

Bài 3.31 trang 72 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Ta cần chứng minh EFGH là hình thoi. Thật vậy:

Do ABCD là hình chữ nhật nên AD = BC.

H là trung điểm của AD nên AH = DH = $\frac{1}{2}$ AD ;

F là trung điểm của BC nên BF = CF = $\frac{1}{2}$ BC

Do đó AH = DH = BF = CF.

Xét $∆$ AHE và $∆$ BFE có:

$\hat{H A E} = \hat{F B E} = 90 °$ ;

AE = BE (do E là trung điểm của AB);

AH = BF (chứng minh trên).

Do đó $∆$ AHE = $∆$ BFE (hai cạnh góc vuông)

Suy ra HE = FE (hai cạnh tương ứng).

Tương tự, ta cũng có:

• $∆$ BEF = $∆$ CGF (hai cạnh góc vuông), suy ra EF = GF (hai cạnh tương ứng).

• $∆$ CGF = $∆$ DGH (hai cạnh góc vuông), suy ra GF = GH (hai cạnh tương ứng).

Từ đó ta có EF = FG = GH = HE

Do đó tứ giác EFHG là hình thoi.

Lời giải bài tập Toán 8 Bài 14: Hình thoi và hình vuông hay, chi tiết khác: