Bài 4.8 trang 83 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8
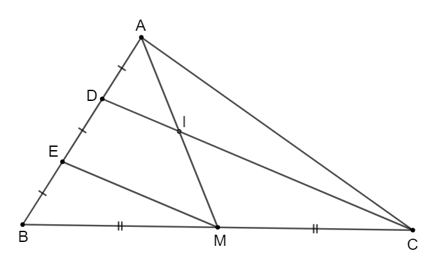
Cho tam giác ABC có trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E.
Giải Toán 8 Bài 16: Đường trung bình của tam giác - Kết nối tri thức
Bài 4.8 trang 83 Toán 8 Tập 1: Cho tam giác ABC có trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E.
a) Chứng minh DC // EM.
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM.
Lời giải:
a) Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.
Ta có BE = DE và E ∈ BD nên E là trung điểm của BD.
Xét tam giác BCD có E, M lần lượt là trung điểm của BD, BC nên EM là đường trung bình của tam giác BCD.
Do đó DC // EM (tính chất đường trung bình).
b) Ta có D là trung điểm của AE (vì AD = DE, D ∈ AE).
Mà DI // EM (vì DC // EM).
Do đó DI là đường trung bình của tam giác AEM.
Suy ra I là trung điểm của AM.
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
HĐ1 trang 82 Toán 8 Tập 1: Cho DE là đường trung bình của tam giác ABC (H.4.15) ....
HĐ2 trang 82 Toán 8 Tập 1: Cho DE là đường trung bình của tam giác ABC (H.4.15) ....