HĐ4 trang 79 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

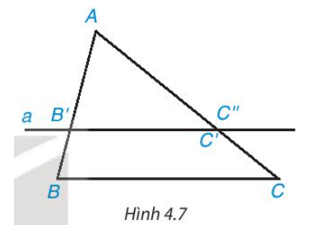
Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm (H.4.7).

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

HĐ4 trang 79 Toán 8 Tập 1: Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm (H.4.7).

• So sánh các tỉ số $\frac{AB\text{'}}{AB}$ và $\frac{AC\text{'}}{AC}$ .

• Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’. Tính độ dài đoạn thẳng AC’’.

• Nhận xét gì về hai điểm C’, C’’ và hai đường thẳng B’C’, BC?

Lời giải:

• Ta có $\frac{AB\text{'}}{AB}=\frac{4}{6}=\frac{2}{3}$; $\frac{AC\text{'}}{AC}=\frac{6}{9}=\frac{2}{3}$ .

Do đó $\frac{AB\text{'}}{AB}=\frac{AC\text{'}}{AC}$ .

• Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên B’C’’ // BC.

Áp dụng định lí Thalès vào ∆ABC, ta có:

$\frac{AB\text{'}}{AB}=\frac{AC\text{'}\text{'}}{AC}$ hay $\frac{4}{6}=\frac{AC\text{'}\text{'}}{9}$ .

Suy ra $AC\text{'}\text{'}=\frac{4.9}{6}=6$(cm).

Vậy AC’’ = 6 cm.

• Trên cạnh AC lấy điểm C’ sao cho AC’ = 6 cm.

Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên điểm C’’ nằm trên cạnh AC sao cho AC’’ = 6 cm.

Do đó, hai điểm C’, C’’ trùng nhau.

Vì hai điểm C’, C’’ trùng nhau mà B’C’’ // BC nên B’C’ // BC.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

• Mở đầu trang 76 Toán 8 Tập 1: Cây cầu AB bắc qua một con sông có chiều rộng 300 m ....

• HĐ1 trang 77 Toán 8 Tập 1: Cho Hình 4.2, em hãy thực hiện các hoạt động sau Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài ....

• HĐ2 trang 77 Toán 8 Tập 1: Cho Hình 4.2, em hãy thực hiện các hoạt động sau Dùng thước thẳng, đo độ dài hai đoạn thẳng AB và CD ....

• HĐ3 trang 77 Toán 8 Tập 1: So sánh hai tỉ số tìm được trong hai hoạt động trên ....

• Luyện tập 1 trang 77 Toán 8 Tập 1: Tìm tỉ số của các đoạn thẳng có độ dài như sau: a) MN = 3 cm và PQ = 9 cm ....

• Luyện tập 2 trang 78 Toán 8 Tập 1: Cho tam giác ABC và một điểm B’ nằm trên cạnh AB. Qua điểm B’, ta vẽ một đường thẳng song song với BC ....

• Luyện tập 3 trang 79 Toán 8 Tập 1: Tìm các độ dài x, y trong Hình 4.6 ....

• Vận dụng trang 80 Toán 8 Tập 1: Em hãy trả lời câu hỏi trong tình huống mở đầu Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông ....

• Bài 4.1 trang 80 Toán 8 Tập 1: Tìm độ dài x, y trong Hình 4.9 (làm tròn kết quả đến chữ số thập phân thứ nhất) ....

• Bài 4.2 trang 80 Toán 8 Tập 1: Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích tại sao chúng song song với nhau ....

• Bài 4.3 trang 80 Toán 8 Tập 1: Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E ....

• Bài 4.4 trang 80 Toán 8 Tập 1: Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M ....

• Bài 4.5 trang 80 Toán 8 Tập 1: Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông ....