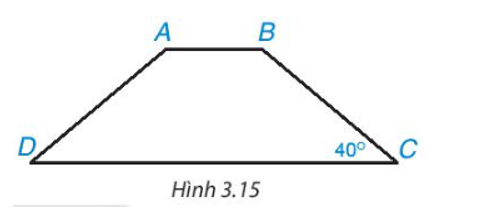
Hình thang cân ABCD (AB song song CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I

Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.

Gọi O là giao điểm của AB và IJ.

Vì ABCD là hình thang cân nên $\widehat{BAD}=\widehat{ABC};\widehat{ADC}=\widehat{BCD};AD=BC;AC=BD$.

Xét ∆ABD và ∆BAC có:

AC = BD (chứng minh trên);

$\widehat{BAD}=\widehat{ABC}$ (chứng minh trên);

AD = BC (chứng minh trên).

Do đó ∆ABD = ∆BAC (c.g.c)

Suy ra $\widehat{ADB}=\widehat{BCD}$ (hai góc tương ứng).

Tam giác ICD cân tại I (vì $\widehat{ADC}=\widehat{BCD}$) nên IC = ID.

Vì $\widehat{ADC}=\widehat{BCD}; \widehat{ABD}=\widehat{BCD}$ nên $\widehat{JDC}=\widehat{JCD}$.

Tam giác JCD cân tại J (vì $\widehat{JDC}=\widehat{JCD}$) nên JC = JD.

Xét ∆IJD và ∆IJC có:

IC = ID (chứng minh trên);

$\widehat{ADB}=\widehat{BCD}$ (chứng minh trên);

JC = JD (chứng minh trên).

Do đó ∆IJD = ∆IJC (c.g.c).

Suy ra $\widehat{DIJ}=\widehat{CIJ}$ (hai góc tương ứng).

Ta có ID = IC, AD = BC.

Mà ID = AI + AD; IC = IB + BC nên IA = IB.

Tam giác IAB cân tại I (vì IA = IB) có IO là tia phân giác $\widehat{AIB}$ 

Suy ra IO là đường trung trực của đoạn thẳng AB.

Vậy đường thẳng IJ là đường trung trực của đoạn thẳng AB.