Hình thoi và hình vuông (Lý thuyết Toán lớp 8) | Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm tóm tắt lý thuyết Toán 8 Bài 14: Hình thoi và hình vuông sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Hình thoi và hình vuông (Lý thuyết Toán lớp 8) | Kết nối tri thức

Lý thuyết Hình thoi và hình vuông

1. Hình thoi

1.1. Khái niệm và tính chất của hình thoi

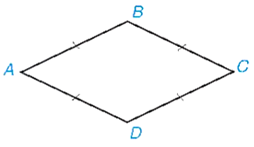
+ Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.

Tứ giác ABCD có AB = BC = CD = DA, nó là một hình thoi.

Chú ý: Hình thoi có tất cả các tính chất của hình bình hành.

+ Định lí 1: Trong hình thoi:

a) Hai đường chéo vuông góc với nhau;

b) Hai đường chéo là các đường phân giác của các góc trong hình thoi.

1.2. Dấu hiệu nhận biết hình thoi

Định lí 2:

a) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

b) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

c) Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

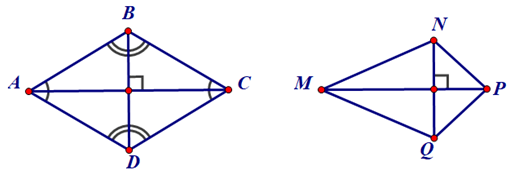
Ví dụ. Trong các hình dưới đây, hình nào là hình thoi?

Hướng dẫn giải

+ Tứ giác ABCD có các góc đối bằng nhau nên là hình bình hành mà hai đường chéo AC và BD vuông góc với nhau nên tứ giác ABCD là hình thoi.

+ Tứ giác MNPQ không là hình thoi vì bốn cạnh không bằng nhau.

2. Hình vuông

2.1. Khái niệm hình vuông và tính chất của nó

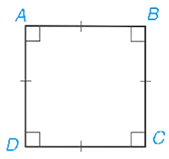
+ Định nghĩa: Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

Tứ giác ABCD có $\hat{A}=\hat{B}=\hat{C}=\hat{D}=90°$  và AB = BC = CD = DA, nó là hình vuông.

+ Định lí 3: Trong một hình vuông, hai đường chéo bằng nhau, vuông góc với nhau, cắt nhau tại trung điểm mỗi đường và là các đường phân giác của các góc của hình vuông.

Chú ý: Hình vuông cũng là hình chữ nhật, hình thoi nên nó có tất cả các tính chất của hình chữ nhật và hình thoi.

2.2. Dấu hiệu nhận biết hình vuông

Định lí 4:

a) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

b) Hình chữ nhật có hai đường chéo vuông góc là hình vuông.

c) Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

Chú ý:

- Hình thoi có một góc vuông là hình vuông.

- Hình thoi có hai đường chéo bằng nhau là hình vuông.

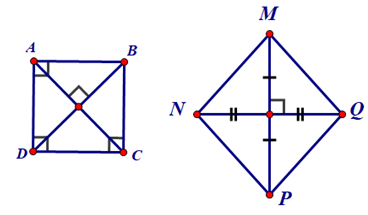
Ví dụ: Tìm hình vuông trong các hình dưới đây:

Hướng dẫn giải

+ Tứ giác ABCD là hình chữ nhật vì có 3 góc vuông, mặt khác hai đường chéo AC và BD vuông góc với nhau nên ABCD là hình vuông.

+ Tứ giác MNPQ không phải là hình chữ nhật vì hai đường chéo không bằng nhau nên nó cũng không phải là hình vuông.

Bài tập Hình thoi và hình vuông

Bài 1. Cho hình bình hành ABCD có AC vuông góc với AD. Gọi E, F theo thứ tự là trung điểm của các cạnh AB, CD. Chứng minh tứ giác AECF là hình thoi.

Hướng dẫn giải

Vì hình bình hành ABCD có AC vuông góc với ADnên $\widehat{CAD}=\widehat{ACB}=90°$.

Xét tam giác vuông CAD vuông tại A có AF là đường trung tuyến ứng với cạnh huyền CD.

Suy ra $AF=\frac{1}{2}CD\Rightarrow AF=FC=FD=\frac{1}{2}CD$  (1)

Tương tự xét tam giác vuông ACB vuông tại C có CE là đường trung tuyến ứng với cạnh huyền AB.

 $\Rightarrow CE=\frac{1}{2}AB\Rightarrow EC=AE=EB=\frac{1}{2}AB$(2)

Lại có: AB = CD (tính chất hình bình hành) (3)

Từ (1), (2) và (3) suy ra AE = CE = CF = FA

Suy ra tứ giác AECF là hình thoi.

Bài 2. Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy hai điểm D, E sao cho BD = DE = EC. Qua D và E kẻ các đường vuông góc với BC, chúng cắt AB, AC lần lượt ở K và H. Tứ giác KHED là hình gì? Vì sao?

Hướng dẫn giải

Vì tam giác ABC vuông cân tại A nên $\hat{B}=\hat{C}=45°$ .

Tam giác DBK vuông tại D có $\hat{B}=45°$  nên tam giác DBK vuông cân tại D.

Suy ra BD = DK (1)

Chứng minh tương tự ta cũng có tam giác EHC vuông cân tại E.

Suy ra EH = EC (2)

Lại có: BD = DE = EC (gt) (3)

Từ (1), (2) và (3) suy ra KD = DE = HE

Tứ giác KHED có KD // HE (cùng vuông góc với BC) và KD = HE nên tứ giác KHED là hình bình hành.

Mặt khác hình bình hành KHED có hai cạnh bên KD = DE nên KHED là hình thoi.

Mà hình thoi KHED có góc KDE là góc vuông (do giả thiết KD vuông góc BC) nên KHED là hình vuông.

Học tốt Hình thoi và hình vuông

Các bài học để học tốt Hình thoi và hình vuông Toán lớp 8 hay khác:

• Giải sgk Toán 8 Bài 14: Hình thoi và hình vuông