Phân tích đa thức thành nhân tử (Lý thuyết Toán lớp 8) | Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm tóm tắt lý thuyết Toán 8 Bài 9: Phân tích đa thức thành nhân tử sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Phân tích đa thức thành nhân tử (Lý thuyết Toán lớp 8) | Kết nối tri thức

Lý thuyết Phân tích đa thức thành nhân tử

1. Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung

Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

Ví dụ 1: Phân tích các đa thức sau thành nhân tử:

a) x² + x;

b) 2x³ + 4x;

c) 3(x + 1) – 4x(x + 1).

Hướng dẫn giải

a) x² + x = x.x + x.1 = x(x + 1);

b) 2x³ + 4x = 2x.x² + 2.2x = 2x(x² + 2);

c) 3(x + 1) – 4x(x + 1) = (x + 1)(3 – 4x).

→ Cách làm như Ví dụ 1 gọi là phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung.

Phương pháp đặt nhân tử chung

+ Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.

+ Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.

Chú ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử.

2. Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức

Ví dụ 2: Phân tích các đa thức sau thành nhân tử:

a) x² + 4x + 4;

b) x² – 9;

c) 27x³ + 1.

Hướng dẫn giải

a) x² + 4x + 4 = x² + 2.x.2 + 2² =(x + 2)²

b) x² – 9 = x² – 3² = (x + 3)(x – 3)

c) 27x³ + 1 = (3x)³ + 1³ = (3x + 1)(9x² – 3x + 1).

→ Cách làm như ví dụ trên được gọi là phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức.

Chú ý:

+ Dùng các hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử.

+ Cần vận dụng linh hoạt các hằng đẳng thức để phù hợp với các nhân tử.

3. Phân tích đa thức thành nhân tử bằng cách nhóm các hạng tử

Ví dụ 3: Phân tích các đa thức sau thành nhân tử:

a) x² – 2xy + 3x – 6y;

b) 2xyz + xy + 2x²z + x².

Hướng dẫn giải

a) x² – 2xy + 3x – 6y = (x²  – 2xy) + (3x – 6y)

                               = x(x – 2y) + 3(x – 2y)

                               = (x – 2y)(x + 3).

b) 2xyz + xy + 2x²z + x² = (2xyz + 2x²z) + (xy + x²)

                                      = 2xz(y + x) + x(y + x)

                                      = (y + x)(2xz + x)

                                      = x(y + x)(2x + 1).

→ Cách làm như trên được gọi là phân tích đa thức thành nhân tử bằng cách nhóm hạng tử.

Phương pháp nhóm hạng tử:

+ Ta vận dụng phương pháp nhóm hạng tử khi không thể phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung hay bằng phương pháp dùng hằng đẳng thức.

+ Ta nhận xét để tìm cách nhóm hạng tử một cách thích hợp (có thể giao hoán và kết hợp các hạng tử để nhóm) sao cho sau khi nhóm, từng nhóm đa thức có thể phân tích được thành nhân tử bằng phương pháp đặt nhân tử chung, bằng phương pháp dùng hằng đẳng thức. Khi đó đa thức mới phải xuất hiện nhân tử chung.

+ Ta áp dụng phương pháp đặt thành nhân tử chung để phân tích đa thức đã cho thành nhân tử.

Chú ý:

+ Đối với một đa thức có thể có nhiều cách nhóm những hạng tử thích hợp.

+ Khi phân tích đa thức thành nhân tử ta phải phân tích đến cuối cùng (không còn phân tích được nữa).

+ Dù phân tích bằng cách nào thì kết quả cũng là duy nhất.

+ Khi nhóm các hạng tử, phải chú ý đến dấu của đa thức.

Bài tập Phân tích đa thức thành nhân tử

Bài 1. Phân tích các đa thức sau thành nhân tử:

a) 3x² + xy;                                                

b) 4x³ – x;

c) x² – 16 + xy – 4y;                                  

d) 8x⁴ – x.

Hướng dẫn giải

a) 3x² + xy = x(3x + y); 

b) 4x³ – x = x(4x² – 1) = x[(2x)² – 1²] = x(2x – 1)(2x + 1);

c) x² – 16 + xy – 4y = (x² – 16) + (xy – 4y)

                             = (x – 4)(x + 4) + y(x – 4)

                             = (x – 4)(x + 4 + y);

d) 8x⁴ – x = x(8x³ – 1) = x[(2x)³ – 1³]

                = x(2x – 1)(4x² + 2x + 1).

Bài 2. Tìm x, biết:

a) 2x² + 2x = 0;                                          

b) 3x³ – 3x = 0.

Hướng dẫn giải

a) Ta có: 2x² + 2x = 2x(x + 1)

Khi đó, 2x² + 2x = 0 thì 2x(x + 1) = 0.

TH1: 2x = 0, suy ra x = 0.

TH2: x + 1 = 0, suy ra x = – 1.

Vậy x = 0 hoặc x = – 1.

b) Ta có: 3x³ – 3x = 3x(x² – 1) = 3x(x – 1)(x + 1).

Khi đó 3x³ – 3x = 0 thì 3x(x + 1)(x – 1) = 0.

TH1: 3x = 0, suy ra x = 0.

TH2: x + 1 = 0, suy ra x = – 1.

TH3: x – 1 = 0, suy ra x = 1.

Vậy x = 0 hoặc x = – 1 hoặc x = 1.

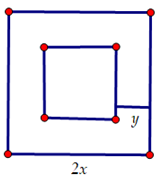
Bài 3. Một khu vườn hình vuông có độ dài cạnh bằng 2x (mét). Người ta làm đường đi xung quanh khu vườn, có độ rộng như nhau và bằng y (mét).

a) Viết biểu thức tính diện tích S của đường đi bao quanh mảnh vườn theo x và y.

b) Phân tích S thành nhân tử rồi tính S khi x = 102 m, y = 4 m.

Hướng dẫn giải

a) Diện tích khu vườn hình vuông là: (2x)² (m²).

Vì làm đường đi bao quanh khu vườn, mỗi bên có độ rộng y mét nên phần vườn không chứa đường đi là một hình vuông có cạnh là 2x – 2y (m).

Diện tích khu vườn hình vuông sau khi làm đường đi là: (2x – 2y)² (m²).

Diện tích đường đi bao quanh khu vườn là: S = (2x)² – (2x – 2y)² (m²).

b) Ta có:

S = (2x)² – (2x – 2y)²

= [2x – (2x – 2y)][2x + (2x – 2y)]

= (2x – 2x + 2y)(2x + 2x – 2y)

= 2y(4x – 2y)

= 4y(2x – y).

Thay x = 102 m, y = 4 m vào S ta được:

S = 4.4.(2.102 – 4) = 16.200 = 3 200 m².

Học tốt Phân tích đa thức thành nhân tử

Các bài học để học tốt Phân tích đa thức thành nhân tử Toán lớp 8 hay khác:

• Giải sgk Toán 8 Bài 9: Phân tích đa thức thành nhân tử