Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y = x và y = –x + 2.

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y = x và y = –x + 2.

a) Vẽ hai đường thẳng đã cho trên cùng mặt phẳng tọa độ.

b) Tìm giao điểm A của hai đường thẳng đã cho.

c) Gọi B là giao điểm của đường thẳng y = –x + 2 và trục Ox. Chứng minh rằng tam giác OAB vuông tại A, tức hai đường thẳng y = x và y = –x + 2 vuông góc với nhau.

d) Có nhận xét gì về tích hai hệ số góc của hai đường thẳng đã cho?

a)

* Xét đường thẳng y = x

Cho x = 1 suy ra y = 1 nên điểm (1; 1) thuộc đường thẳng y = x.

Đường thẳng y = x đi qua 2 điểm O(0; 0) và (1; 1).

* Xét đường thẳng y = –x + 2

Cho y = 0 thì x = 2 nên điểm (2; 0) thuộc đường thẳng y = – x + 2.

Cho x = 0 thì y = 2 nên điểm (0; 2 ) thuộc đường thẳng y = –x + 2.

Đường thẳng y = – x + 2 đi qua hai điểm (2; 0) và (0; 2).

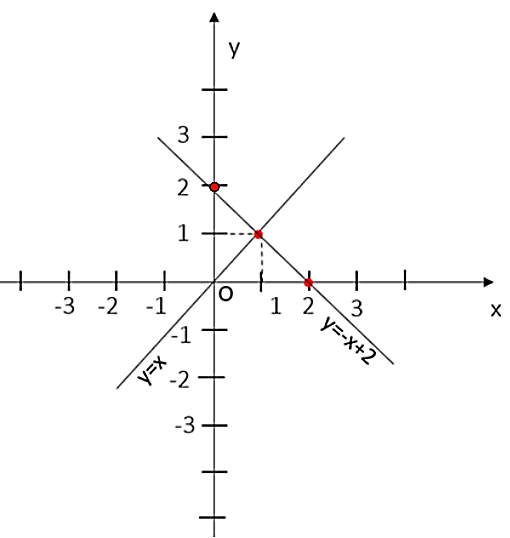
b) Phương trình hoành độ giao điểm của hai đường thẳng đã cho là:

x = –x + 2

Giải phương trình này ta được x = 1. Từ đó suy ra y = 1.

Vậy tọa độ giao điểm A(1; 1).

c) Giao điểm của đường thẳng y = –x + 2 và trục Ox là B(2; 0).

Gọi C là giao điểm của đường thẳng y = –x + 2 và trục Oy. Suy ra C(0; 2).

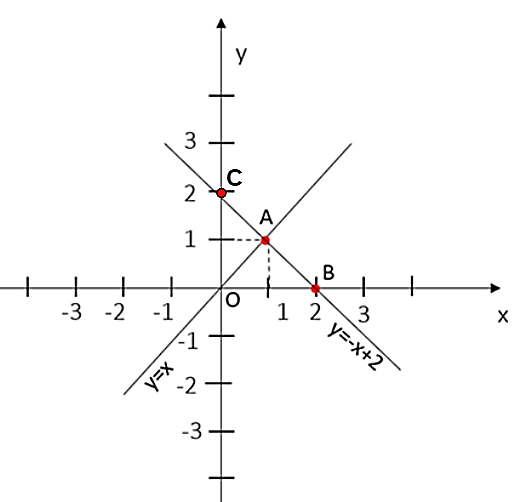
Dễ thấy tam giác OBC vuông cân tại O (vì OB = OC = 2).

Xét hai tam giác OAB và OAC có:

Cạnh OA chung;

OB = OC;

 $\widehat{OBA}$= $\widehat{OCA}=45°$

Do đó ΔOAB = ΔOAC, từ đó suy ra AB = AC.

Điều này chứng tỏ A là trung điểm của BC, mà ΔOBC cân tại O nên OA ⊥ AB, tức là ΔOAB vuông tại A.

d) Đường thẳng y = x có hệ số góc bằng 1.

Đường thẳng y = – x + 1 có hệ số góc bằng –1.

Tích của hai hệ số góc của hai đường thẳng đã cho bằng –1.

Từ câu c), ta có nhận xét: