Bài 3 trang 124 Toán 9 Tập 1 Cánh diều
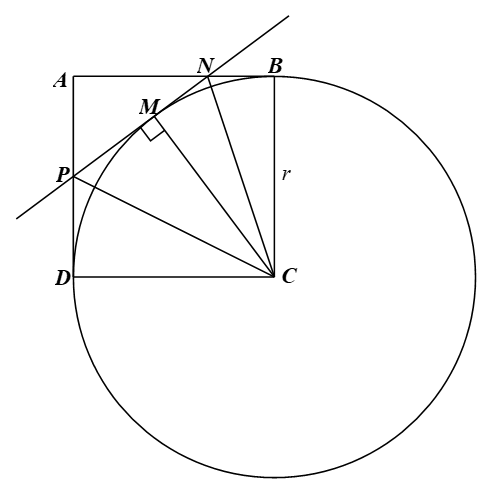
Cho hình vuông ABCD cạnh r và đường tròn (C; r). Giả sử M là một điểm nằm trên đường tròn (C; r) sao cho điểm M nằm trong hình vuông ABCD. Tiếp tuyến của đường tròn (C; r) tại tiếp điểm M cắt các đoạn thẳng AB, AD lần lượt tại N, P. Chứng minh:
Giải Toán 9 Bài tập cuối chương 5 - Cánh diều
Bài 3 trang 124 Toán 9 Tập 1: Cho hình vuông ABCD cạnh r và đường tròn (C; r). Giả sử M là một điểm nằm trên đường tròn (C; r) sao cho điểm M nằm trong hình vuông ABCD. Tiếp tuyến của đường tròn (C; r) tại tiếp điểm M cắt các đoạn thẳng AB, AD lần lượt tại N, P. Chứng minh:
a) Các đường thẳng NB, PD là các tiếp tuyến của đường tròn (C; r).
b)
Lời giải:
a) Vì ABCD là hình vuông nên ta có
Hay CB ⊥ AB tại B và CD ⊥ AD tại D.
Mà CB và CD là bán kính của đường tròn (C; r) và B ∈ (C; r); D ∈ (C; r).
Suy ra AB, AD là các tiếp tuyến của đường tròn (C; r).
Vậy các đường thẳng NB, PD là các tiếp tuyến của đường tròn (C; r).
b) Xét đường tròn (C; r) có hai tiếp tuyến PM và PD cắt nhau tại P nên PC là tia phân giác của Suy ra
Tương tự, MN và NB là hai tiếp tuyến của đường tròn (C; r) cắt nhau tại N nên CN là tia phân giác của Suy ra
Lại có:
Suy ra nên
Do đó
Vậy
Lời giải bài tập Toán 9 Bài tập cuối chương 5 hay, chi tiết khác:
Bài 1 trang 124 Toán 9 Tập 1: Trong Hình 92, cho các điểm A, B, C, D, E thuộc đường tròn (O) ....
Bài 2 trang 124 Toán 9 Tập 1: a) Độ dài cung tròn có số đo 30° của đường tròn bán kính R là: ....
Bài 4 trang 124 Toán 9 Tập 1: Chứng minh trong một đường tròn: ....
Bài 5 trang 124 Toán 9 Tập 1: Cho hai đường tròn (I; r) và (K; R) tiếp xúc ngoài với nhau tại P ....