Bài 4 trang 124 Toán 9 Tập 1 Cánh diều
Chứng minh trong một đường tròn:
Giải Toán 9 Bài tập cuối chương 5 - Cánh diều
Bài 4 trang 124 Toán 9 Tập 1: Chứng minh trong một đường tròn:
a) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy;
b) Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy;
c) Hai dây bằng nhau thì cách đều tâm;
d) Hai dây cách đều tâm thì bằng nhau.
Lời giải:
a)
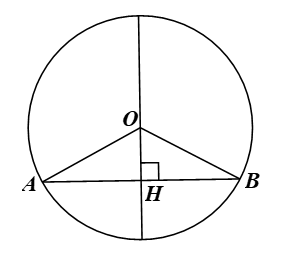
Gọi (O) là đường tròn có đường kính vuông góc với dây AB tại H.
Xét ∆OAB có OA = OB = R nên ∆OAB cân tại O.
∆OAB cân tại O có OH là đường cao (do OH ⊥ AB) nên đồng thời là đường trung tuyến của tam giác. Do đó H là trung điểm của AB.
Vậy đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
b)
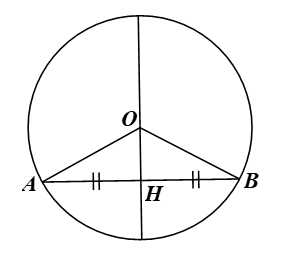
Gọi (O) là đường tròn có đường kính đi qua trung điểm H của dây AB.
Xét ∆OAB có OA = OB = R nên ∆OAB cân tại O.
∆OAB cân tại O có OH là đường trung tuyến nên đồng thời là đường cao của tam giác. Do đó OH ⊥ AB tại H.
Vậy đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
c)
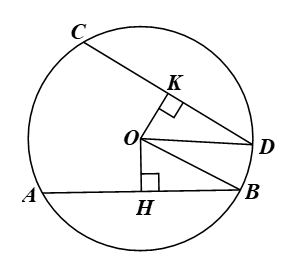
Gọi (O) là đường tròn có hai dây AB, CD. Gọi OH, OK lần lượt là khoảng cách từ O đến AB, CD. Khi đó OH ⊥ AB tại H và OK ⊥ CD tại K.
Do đó, theo kết quả của câu a, ta có: H, K lần lượt là trung điểm của AB, CD.
Suy ra HB = AB và KD = CD.
Mà AB = CD nên HB = KD. (1)
Xét ∆OHB vuông tại H, ta có: OB2 = OH2 + HB2 (định lí Pythagore).
Suy ra OH2 = OB2 – HB2 = R2 – HB2. (2)
Xét ∆OKD vuông tại H, ta có: OD2 = OK2 + KD2 (định lí Pythagore).
Suy ra OK2 = OD2 – KD2 = R2 – KD2. (3)
Từ (1), (2) và (3) suy ra OH2 = OK2, hay OH = OK.
Vậyhai dây bằng nhau thì cách đều tâm.
d)
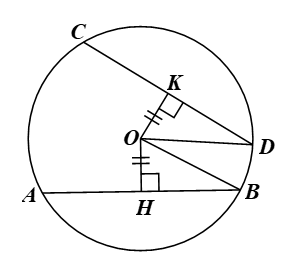
Gọi (O) là đường tròn có hai dây AB, CD bằng nhau. Gọi OH, OK lần lượt là khoảng cách từ O đến AB, CD. Khi đó OH ⊥ AB tại H, OK ⊥ CD tại K.
Do đó, theo kết quả của câu a, ta có: H, K lần lượt là trung điểm của AB, CD.
Suy ra AB = 2HB và CD = 2KD.
Theo bài, OH = OK, suy ra OH2 = OK2. (1)
Xét ∆OHB vuông tại H, ta có: OB2 = OH2 + HB2 (định lí Pythagore).
Suy ra HB2 = OB2 – OH2 = R2 – OH2. (2)
Xét ∆OKD vuông tại H, ta có: OD2 = OK2 + KD2 (định lí Pythagore).
Suy ra KD2 = OD2 – OK2 = R2 – OK2. (3)
Từ (1), (2) và (3) suy ra HB2 = KD2, hay HB = KD.
Do đó 2HB = 2KD hay AB = CD.
Vậy hai dây cách đều tâm thì bằng nhau.
Lời giải bài tập Toán 9 Bài tập cuối chương 5 hay, chi tiết khác:
Bài 1 trang 124 Toán 9 Tập 1: Trong Hình 92, cho các điểm A, B, C, D, E thuộc đường tròn (O) ....
Bài 2 trang 124 Toán 9 Tập 1: a) Độ dài cung tròn có số đo 30° của đường tròn bán kính R là: ....
Bài 3 trang 124 Toán 9 Tập 1: a) Vì ABCD là hình vuông nên ta có ....
Bài 5 trang 124 Toán 9 Tập 1: Cho hai đường tròn (I; r) và (K; R) tiếp xúc ngoài với nhau tại P ....