Bài 7 trang 78 Toán 9 Tập 2 Cánh diều

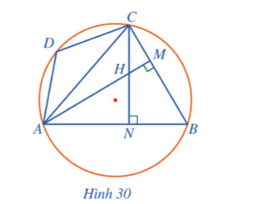
Cho tứ giác nội tiếp ABCD có tam giác ABC là tam giác nhọn. Hai đường cao AM và CN của tam giác ABC cắt nhau tại H (Hình 30).

Giải Toán 9 Bài 2: Tứ giác nội tiếp đường tròn - Cánh diều

Bài 7 trang 78 Toán 9 Tập 2: Cho tứ giác nội tiếp ABCD có tam giác ABC là tam giác nhọn. Hai đường cao AM và CN của tam giác ABC cắt nhau tại H (Hình 30).

Chứng minh:

a) $\widehat{MHN}+\widehat{ABC}=180°;$

b) $\widehat{AHC}=\widehat{ADC};$

c) $\widehat{ADC}=\widehat{BAM}+90°.$

Lời giải:

a) Xét ∆ABC có hai đường cao AM và CN cắt nhau tại H nên AM ⊥ BC và CN ⊥ AB, do đó $\widehat{HMB}=90°,\widehat{HNB}=90°.$

Xét tứ giác HMBN có:

$\widehat{MHN}+\widehat{HMB}+\widehat{MBN}+\widehat{HNB}=360°$ (tổng các góc của một tứ giác)

Suy ra $\widehat{MHN}+\widehat{MBN}=360°-\widehat{HMB}-\widehat{HNB}=360°-90°-90°=180°.$

Hay $\widehat{MHN}+\widehat{ABC}=180°.$

b) Vì tứ giác ABCD là tứ giác nội tiếp nên tổng hai góc đối nhau bằng 180°.

Do đó $\widehat{ADC}+\widehat{ABC}=180°.$

Mà $\widehat{MHN}+\widehat{ABC}=180°$ (câu a) nên $\widehat{MHN}=\widehat{ADC}.$

Lại có $\widehat{MHN}=\widehat{AHC}$ (đối đỉnh) nên $\widehat{AHC}=\widehat{ADC}.$

c) Xét ∆AHN vuông tại N có $\widehat{AHC}$ là góc ngoài của tam giác tại đỉnh H nên $\widehat{AHC}=\widehat{HAN}+\widehat{HNA}=\widehat{BAM}+90°$ (tính chất góc ngoài của một tam giác).

Mà $\widehat{AHC}=\widehat{ADC}$ (câu b) nên $\widehat{ADC}=\widehat{BAM}+90°.$

Lời giải bài tập Toán 9 Bài 2: Tứ giác nội tiếp đường tròn hay, chi tiết khác:

• Khởi động trang 75 Toán 9 Tập 2: Hình 19 minh họa một đường tròn và tứ giác ABCD có bốn đỉnh thuộc đường tròn.....

• Hoạt động 1 trang 75 Toán 9 Tập 2: Quan sát Hình 20 và cho biết các đỉnh của tứ giác ABCD có thuộc đường tròn (O) hay không....

• Luyện tập 1 trang 75 Toán 9 Tập 2: Dùng thước thẳng và compa vẽ một tứ giác nội tiếp đường tròn theo các bước sau:Vẽ một đường tròn;....

• Hoạt động 2 trang 76 Toán 9 Tập 2: Trong Hình 22, cho biết $\widehat{AOC}=\alpha .$Tính số đo của các cung và góc sau theo α:....

• Luyện tập 2 trang 76 Toán 9 Tập 2: Cho đường tròn (O) ngoại tiếp tam giác đều ABC và điểm M thuộc cung nhỏ BC (M khác B và C). Tính số đo góc BMC....

• Hoạt động 3 trang 76 Toán 9 Tập 2: Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R = OA và vẽ đường tròn (O; R). Các điểm A, B, C, D có thuộc (O; R) hay không?...

• Luyện tập 3 trang 77 Toán 9 Tập 2: Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 8 cm và 6 cm....

• Hoạt động 4 trang 77 Toán 9 Tập 2: Cho hình vuông ABCD, AC cắt BD tại điểm O (Hình 20). a) Mỗi đường chéo của hình vuông ABCD có phải là đường kính của đường tròn ngoại tiếp hình vuông đó hay không?....

• Luyện tập 4 trang 77 Toán 9 Tập 2: Tính tỉ số giữa chu vi của một hình vuông và chu vi của đường tròn ngoại tiếp hình vuông đó. ....

• Bài 1 trang 78 Toán 9 Tập 2: Quan sát Hình 28 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tứ giác ABCD, đường tròn nào ngoại tiếp tứ giác ABMN....

• Bài 2 trang 78 Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn. Tính số đo các góc còn lại của tứ giác đó trong mỗi trường hợp sau:....

• Bài 3 trang 78 Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O) thoả mãn $\widehat{ABC}=60°,$$\widehat{ACB}=70°.$ Giả sử D là điểm thuộc cung BC không chứa A (D khác B và C).....

• Bài 4 trang 78 Toán 9 Tập 2: Mặt trên của tấm đệm có dạng hình tròn ở Hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng....

• Bài 5 trang 78 Toán 9 Tập 2: Cho hình thang ABCD (AB // CD) nội tiếp đường tròn. Chứng minh rằng hình thang ABCD là hình thang cân.....

• Bài 6 trang 78 Toán 9 Tập 2: Cho tứ giác nội tiếp ABCD có hai đường chéo AC và BD cắt nhau tại I. a) Hai góc ABD và ACD có bằng nhau hay không? Vì sao?....