Luyện tập 2 trang 76 Toán 9 Tập 2 Cánh diều

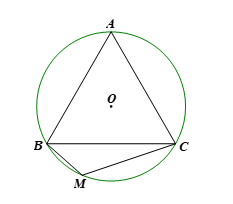
Cho đường tròn (O) ngoại tiếp tam giác đều ABC và điểm M thuộc cung nhỏ BC (M khác B và C). Tính số đo góc BMC.

Giải Toán 9 Bài 2: Tứ giác nội tiếp đường tròn - Cánh diều

Luyện tập 2 trang 76 Toán 9 Tập 2: Cho đường tròn (O) ngoại tiếp tam giác đều ABC và điểm M thuộc cung nhỏ BC (M khác B và C). Tính số đo góc BMC.

Lời giải:

Vì tam giác ABC đều nên $\widehat{BAC}=60°.$

Vì 4 điểm A, B, M, C cùng nằm trên đường tròn (O) nên tứ giác ABMC là tứ giác nội tiếp đường tròn (O).

Do đó tổng số đo hai góc đối của tứ giác ABMC bằng 180°.

Suy ra $\widehat{BAC}+\widehat{BMC}=180°$

Nên $\widehat{BMC}=180°-\widehat{BAC}=180°-60°=120°.$

Vậy $\widehat{BMC}=120°.$

Lời giải bài tập Toán 9 Bài 2: Tứ giác nội tiếp đường tròn hay, chi tiết khác:

• Khởi động trang 75 Toán 9 Tập 2: Hình 19 minh họa một đường tròn và tứ giác ABCD có bốn đỉnh thuộc đường tròn.....

• Hoạt động 1 trang 75 Toán 9 Tập 2: Quan sát Hình 20 và cho biết các đỉnh của tứ giác ABCD có thuộc đường tròn (O) hay không....

• Luyện tập 1 trang 75 Toán 9 Tập 2: Dùng thước thẳng và compa vẽ một tứ giác nội tiếp đường tròn theo các bước sau:Vẽ một đường tròn;....

• Hoạt động 2 trang 76 Toán 9 Tập 2: Trong Hình 22, cho biết $\widehat{AOC}=\alpha .$Tính số đo của các cung và góc sau theo α:....

• Hoạt động 3 trang 76 Toán 9 Tập 2: Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R = OA và vẽ đường tròn (O; R). Các điểm A, B, C, D có thuộc (O; R) hay không?...

• Luyện tập 3 trang 77 Toán 9 Tập 2: Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 8 cm và 6 cm....

• Hoạt động 4 trang 77 Toán 9 Tập 2: Cho hình vuông ABCD, AC cắt BD tại điểm O (Hình 20). a) Mỗi đường chéo của hình vuông ABCD có phải là đường kính của đường tròn ngoại tiếp hình vuông đó hay không?....

• Luyện tập 4 trang 77 Toán 9 Tập 2: Tính tỉ số giữa chu vi của một hình vuông và chu vi của đường tròn ngoại tiếp hình vuông đó. ....

• Bài 1 trang 78 Toán 9 Tập 2: Quan sát Hình 28 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tứ giác ABCD, đường tròn nào ngoại tiếp tứ giác ABMN....

• Bài 2 trang 78 Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn. Tính số đo các góc còn lại của tứ giác đó trong mỗi trường hợp sau:....

• Bài 3 trang 78 Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O) thoả mãn $\widehat{ABC}=60°,$$\widehat{ACB}=70°.$ Giả sử D là điểm thuộc cung BC không chứa A (D khác B và C).....

• Bài 4 trang 78 Toán 9 Tập 2: Mặt trên của tấm đệm có dạng hình tròn ở Hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng....

• Bài 5 trang 78 Toán 9 Tập 2: Cho hình thang ABCD (AB // CD) nội tiếp đường tròn. Chứng minh rằng hình thang ABCD là hình thang cân.....

• Bài 6 trang 78 Toán 9 Tập 2: Cho tứ giác nội tiếp ABCD có hai đường chéo AC và BD cắt nhau tại I. a) Hai góc ABD và ACD có bằng nhau hay không? Vì sao?....

• Bài 7 trang 78 Toán 9 Tập 2: Cho tứ giác nội tiếp ABCD có tam giác ABC là tam giác nhọn. Hai đường cao AM và CN của tam giác ABC cắt nhau tại H (Hình 30). ....