Giải Toán 9 trang 61 Tập 1 Cánh diều

---

Với Giải Toán 9 trang 61 Tập 1 trong Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số Toán lớp 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 61.

Giải Toán 9 trang 61 Tập 1 Cánh diều

Khởi động trang 61 Toán 9 Tập 1:

Để lái xe an toàn khi đi qua đoạn đường có dạng cung tròn, người lái cần biết tốc độ tối đa cho phép là bao nhiêu. Vì thế, ở những đoạn đường đó thường có bảng chỉ dẫn cho tốc độ tối đa cho phép của ô tô. Tốc độ tối đa cho phép v (m/s) được tính bởi công thức $v=\sqrt{rg\mu },$ trong đó r (m) là bán kính của cung đường, g = 9,8 m/s², μ là hệ số ma sát trượt của đường.

(Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017)

Hãy viết biểu thức tính v theo r khi biết μ = 0,12.

Trong toán học, biểu thức đó được gọi là gì?

Lời giải:

Theo bài, g = 9,8 m/s² vàμ = 0,12.

Thay vào biểu thức $v=\sqrt{rg\mu },$ ta được: $v=\sqrt{r\cdot 9,8\cdot 0,12}=\sqrt{1,176r}$ (m/s).

Vậy biểu thức tính v theo r là $v=\sqrt{1,176r}$ (m/s).

Trong toán học, biểu thứ trên được gọi là căn thức bậc hai.

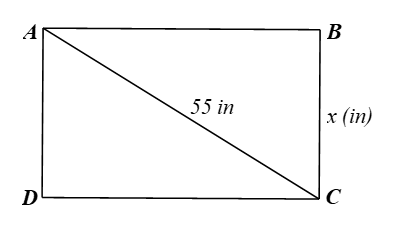
Hoạt động 1 trang 61 Toán 9 Tập 1: Cửa hàng điện máy trưng bày một chiếc ti vi màn hình phẳng 55 in, tức là độ dài đường chéo của màn hình ti vi bằng 55 in (1 in = 2,54 cm). Gọi x (in) là chiều rộng của màn hình ti vi (Hình 5).

Viết công thức tính chiều dài của màn hình ti vi theo x.

Lời giải:

Giả sử hình ảnh chiếc ti vi được mô tả như hình vẽ dưới đây:

Áp dụng định lí Pythagore cho ∆ABC vuông tại B, ta có:

AC² = AB² + BC²

Suy ra AB² = AC² – BC² = 55² – x²

Do đó AB = $\sqrt{{55}^2-x^2}$ (in).

Vậy công thức tính chiều dài của màn hình ti vi là $\sqrt{{55}^2-x^2}$ (in).

Lời giải bài tập Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số hay khác:

• Giải Toán 9 trang 62

• Giải Toán 9 trang 63

• Giải Toán 9 trang 64

• Giải Toán 9 trang 65

• Giải Toán 9 trang 66