b) Tính số đo của mỗi góc ở tâm tìm được ở câu a.
Câu hỏi:
b) Tính số đo của mỗi góc ở tâm tìm được ở câu a.
Trả lời:
b) Ta có: Suy ra:
⦁
⦁
Ta có Suy ra
Vậy
Câu hỏi:
b) Tính số đo của mỗi góc ở tâm tìm được ở câu a.
Trả lời:
b) Ta có: Suy ra:
⦁
⦁
Ta có Suy ra
Vậy
Câu 1:
Cho hai đường tròn (O; 5 cm), (O’; 4 cm) với OO’ = 9 cm. Kết luận nào sau đây đúng về vị trí tương đối của hai đường tròn?
A. Hai đường tròn cắt nhau.
B. Hai đường tròn ở ngoài nhau.
C. Hai đường tròn tiếp xúc ngoài.
D. Hai đường tròn tiếp xúc trong.
Câu 2:
Cho đường tròn (O; 6 cm) và đường thẳng a với khoảng cách từ O đến a là 4 cm. Kết luận nào sau đây đúng về vị trí giữa đường tròn (O) và đường thẳng a?
A. (O) và a cắt nhau tại hai điểm.
B. (O) và a tiếp xúc.
C. (O) và a không có điểm chung.
D. (O) và a có duy nhất điểm chung.
Câu 3:
Góc ở tâm là góc
A. có đỉnh nằm trên đường tròn
B. có đỉnh nằm trên bán kính của đường tròn.
C. có hai cạnh là hai đường kính của đường tròn.
D. có đỉnh trùng với tâm đường tròn.
Câu 4:
Hình nào dưới đây biểu diễn góc nội tiếp?
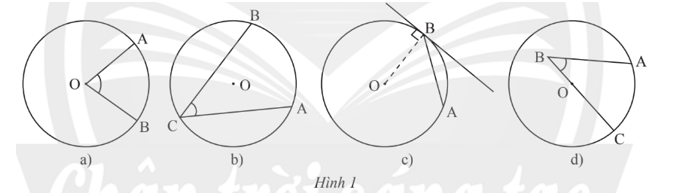
A. Hình 1a.
B. Hình 1b.
C. Hình 1c.
D. Hình 1d.
Câu 7:
Hãy hoàn thành bảng số liệu sau vào vở (lấy π ≈ 3,14 và làm tròn kết quả đến hàng phần mười).
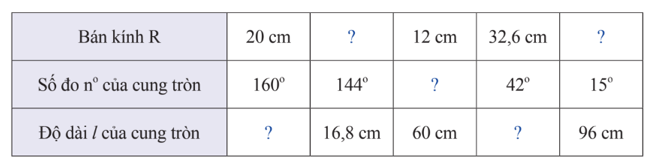
Câu 8:
Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O’) đường kính BC.
a) Chứng minh rằng hai đường tròn (O) và (O’) tiếp xúc ngoài tại B.
