Bài 5 trang 74 Toán 9 Tập 2 Chân trời sáng tạo
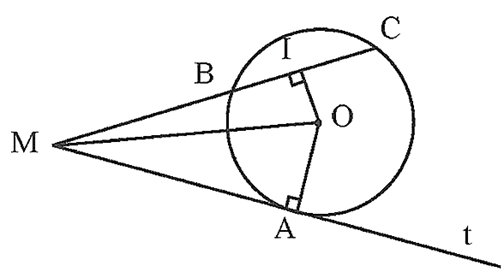
Từ một điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O) tại A. Gọi I là trung điểm của dây BC. Chứng minh AMIO là một tứ giác nội tiếp.
Giải Toán 9 Bài 2: Tứ giác nội tiếp - Chân trời sáng tạo
Bài 5 trang 74 Toán 9 Tập 2: Từ một điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O) tại A. Gọi I là trung điểm của dây BC. Chứng minh AMIO là một tứ giác nội tiếp.
Lời giải:
Vì MA là tiếp tuyến của (O) nên MA ⊥ OA hay
Vì I là trung điểm của BC của ∆OBC cân tại O nên OI ⊥ BC hay
Ta có ∆OAM vuông tại A và ∆OIM vuông tại I cùng nội tiếp đường tròn đường kính MO.
Suy ra AMIO là tứ giác nội tiếp đường tròn đường kính MO.
Lời giải bài tập Toán 9 Bài 2: Tứ giác nội tiếp hay, chi tiết khác:
Khám phá 1 trang 70 Toán 9 Tập 2: Các tứ giác trong Hình 1 có đặc điểm gì giống nhau? ....
Khám phá 2 trang 71 Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4) ....
Thực hành 2 trang 71 Toán 9 Tập 2: Tìm số đo các góc chưa biết của tứ giác ABCD trong Hình 6 ....
Vận dụng 2 trang 71 Toán 9 Tập 2: Trong hình vẽ minh họa của học sinh có một tứ giác ABCD ....
Khám phá 3 trang 72 Toán 9 Tập 2: Cho hình chữ nhật ABCD và hình vuông MNPQ (Hình 8) ....
Bài 1 trang 73 Toán 9 Tập 2: Cho ABCD là tứ giác nội tiếp. Hãy hoàn thành bảng sau vào vở ....
Bài 3 trang 74 Toán 9 Tập 2: Xác định tâm và bán kính đường tròn ngoại tiếp hình chữ nhật ABCD ....