Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF?
Câu hỏi:
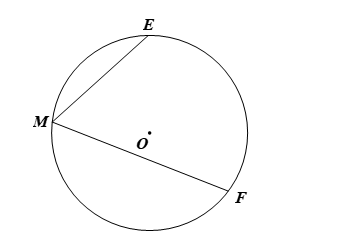
Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF?
Trả lời:
Có vô số góc nội tiếp chắn cung EF vì với mỗi điểm M (khác E và F) nằm trên đường tròn (O) thì ta có một góc nội tiếp.
Xem thêm lời giải bài tập Toán 9 Chân trời sáng tạo hay, chi tiết:
Câu 1:
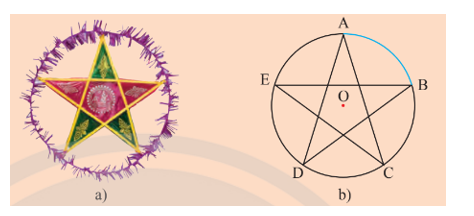
Hình ngôi sao năm cánh trong Hình a được vẽ lại như Hình b. Phần tô màu xanh trên đường tròn từ điểm A đến điểm B được gọi là gì? Làm thế nào để biểu diễn số đo của nó?
Xem lời giải »
Câu 2:
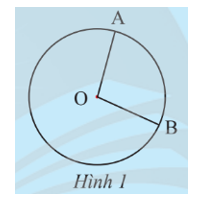
Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của
Xem lời giải »
Câu 3:
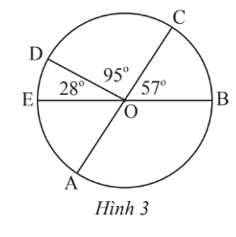
Tính số đo góc ở tâm và trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O).
Xem lời giải »
Câu 4:
Tính số đo góc ở tâm được tạo thành khi kim giờ quay:
a) Từ 7 giờ đến 9 giờ;
b) Từ 9 giờ đến 12 giờ.
Xem lời giải »
Câu 5:
Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB.
Xem lời giải »
Câu 6:
Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung
Xem lời giải »