Cho hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D, AB = 8 cm. Gọi K,I
Câu hỏi:
Cho hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D, AB = 8 cm. Gọi K, I lần lượt là giao điểm của hai đường tròn đã cho với đoạn thẳng AB (Hình 21).
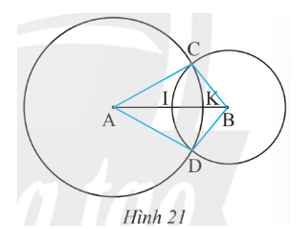
a) Tính độ dài của các đoạn thẳng CA, CB, DA và DB.
b) Điểm I có phải là trung điểm của đoạn thẳng AB không?
c) Tính độ dài của đoạn thẳng IK.
Trả lời:
a) Vì hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D nên C, D cùng nằm trên hai đường tròn (A; 6 cm) và (B; 4 cm), do đó AC = AD = 6 cm và BC = BD = 4 cm.
b) Do I là giao điểm của đường tròn (B; 4 cm) với đoạn thẳng AB nên I nằm giữa hai điểm A, B và I nằm trên đường tròn (B; 4 cm), do đó BI = 4 cm.
Vì I nằm giữa hai điểm A, B nên ta có: AI + IB = AB
Suy ra AI = AB – IB = 8 – 4 = 4 (cm).
Ta có I nằm giữa hai điểm A, B và AI = BI nên I là trung điểm của đoạn thẳng AB.
c) Do K là giao điểm của đường tròn (A; 6 cm) với đoạn thẳng AB nên K nằm trên đường tròn (A; 6 cm), do đó AK = 6 cm.
Ta có AI < AK (4 cm < 6 cm) nên I nằm giữa hai điểm A, K.
Do đó AI + IK = AK
Suy ra IK = AK – AI = 6 – 4 = 2 (cm).
Vậy IK = 2 cm.