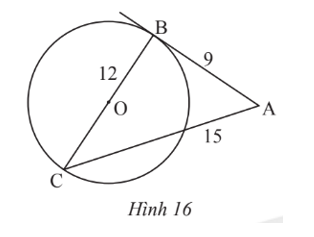
Trong Hình 16, AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O).
Câu hỏi:
Trong Hình 16, AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).
Trả lời:
Xét ∆ABC có:
⦁ AB2 + BC2 = 92 + 122 = 225;
⦁ AC2 = 152 = 225.
Do đó AB2 + BC2 = AC2,
Theo định lí Pythagore đảo, ta có ∆ABC vuông tại B.
Suy ra AB ⊥ BC hay AB ⊥ OB.
Xét đường tròn (O) có AB ⊥ OB tại B thuộc đường tròn (O) nên AB là tiếp tuyến của đường tròn (O).
Xem thêm lời giải bài tập Toán 9 Chân trời sáng tạo hay, chi tiết:
Câu 1:
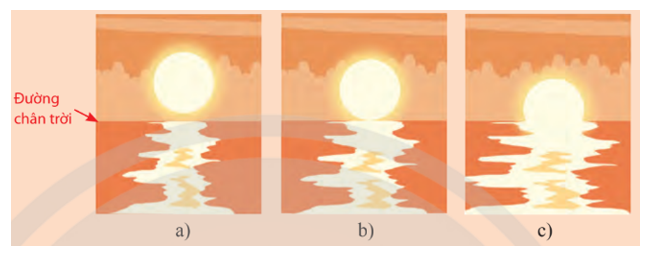
Hãy mô tả các vị trí của Mặt Trời so với đường chân trời ở các thời điểm Mặt Trời lặn khác nhau trong hình dưới đây.
Xem lời giải »
Câu 2:
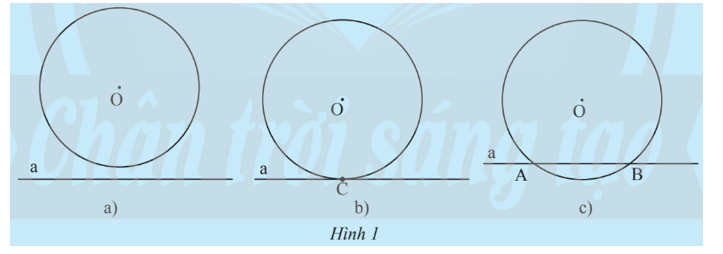
Nêu nhận xét về số điểm chung của đường thẳng a và đường tròn (O) trong mỗi hình sau:
Xem lời giải »
Câu 3:
Cho đường tròn (J; 5 cm) và đường thẳng c. Gọi K là chân đường vuông góc vẽ từ J xuống c, d là độ dài của đoạn thẳng JK. Xác định vị trí tương đối của đường thẳng c và đường tròn (J; 5 cm) trong mỗi trường hợp sau:
a) d = 4 cm;
b) d = 5 cm;
c) d = 6 cm.
Xem lời giải »
Câu 4:
Một diễn viên xiếc đi xe đạp một bánh trên sợi dây cáp căng được cố định ở hai đầu dây. Biết đường kính bánh xe là 72 cm, tính khoảng cách từ trục bánh xe đến dây cáp.
Xem lời giải »
Câu 5:
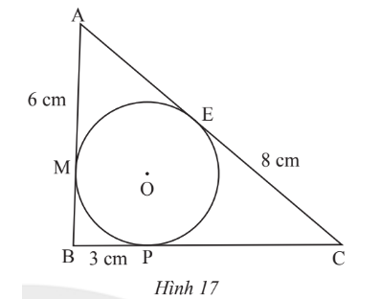
Cho tam giác ABC có đường tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm, BP = 3 cm, CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.
Xem lời giải »