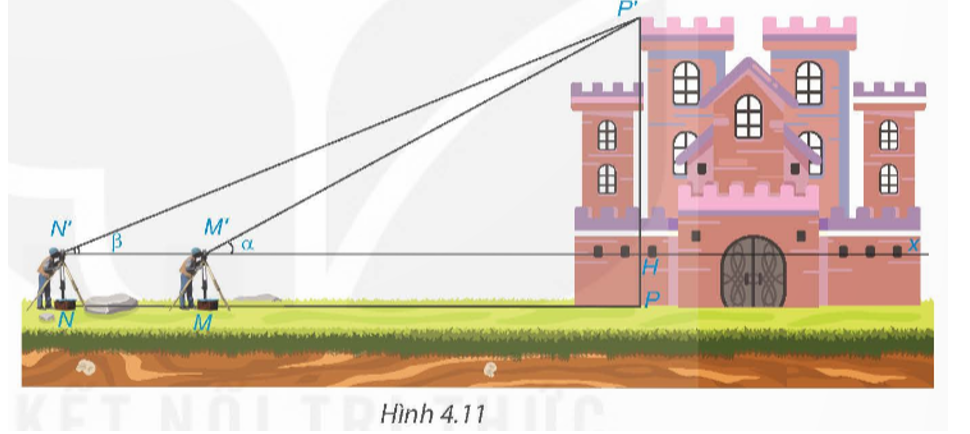
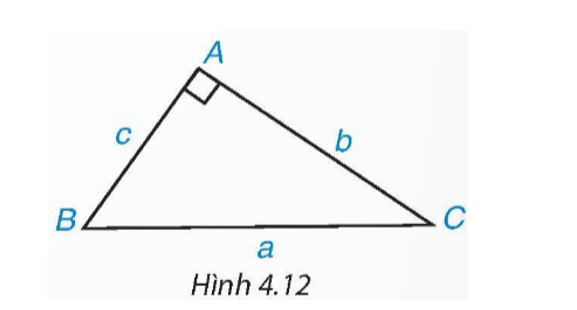
2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB
Câu hỏi:
2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.
Trả lời:
2.
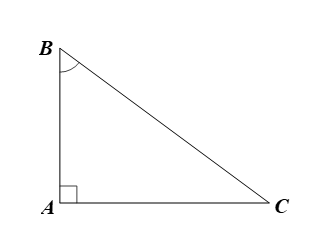
Trường hợp biết cạnh góc vuông AB và góc B, ta cần tính số đo góc C và các cạnh AC, BC:
Ta tính được góc C thông qua định lí tổng ba góc của một tam giác.
Xét ∆ABC vuông tại A, sử dụng định lí 1, ta có: AB = BC.cosB, suy ra
Sử dụng định lí 2, ta có AC = AB.tanB.
Trường hợp biết biết cạnh huyền BC và góc B, ta cần tính số đo góc C và các cạnh AB, AC:
Ta tính được góc C thông qua định lí tổng ba góc của một tam giác.
Xét ∆ABC vuông tại A, sử dụng định lí 1, ta có: AB = BC.cosB và AC = BC.sinB.
Lưu ý: Ngoài cách giải đã nêu, ta cũng có nhiều cách giải khác cho bài toán.