Bài 5.3 trang 86 Toán 9 Kết nối tri thức Tập 1
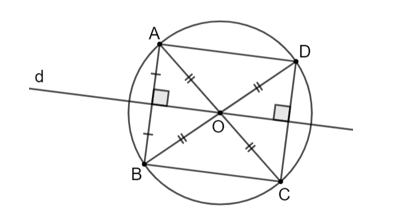
Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d, C và D lần lượt là điểm đối xứng với A và B qua O.
Giải Toán 9 Bài 13: Mở đầu về đường tròn - Kết nối tri thức
Bài 5.3 trang 86 Toán 9 Tập 1: Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d, C và D lần lượt là điểm đối xứng với A và B qua O.
a) Ba điểm B, C và D có thuộc (O) hay không? Vì sao?
b) Chứng minh tứ giác ABCD là hình chữ nhật.
c) Chứng minh rằng C và D đối xứng với nhau qua d.
Lời giải:
a) Ta có d là là đường thẳng đi qua tâm O nên d là trục đối xứng của đường tròn.
Vì A thuộc (O) và B là điểm đối xứng của A qua d nên B cũng thuộc (O).
Vì C, D lần lượt là điểm đối xứng của A, B qua O nên C, D cũng thuộc (O).
b) C đối xứng với A qua O nên O là trung điểm của AC.
D đối xứng với B qua O nên O là trung điểm của BD.
Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường.
Mà BD = CD (bằng 2 lần bán kính (O)).
Do đó, tứ giác ABCD là hình chữ nhật.
c) Vì ABCD là hình chữ nhật nên AB // CD, mà AB ⊥ d nên d ⊥ CD.
Xét tam giác OCD có OC = OD nên tam giác OCD cân tại O.
Mà đường thẳng d là đường cao của tam giác OCD nên d cũng là trung trực của CD. Hay C và D đối xứng nhau qua đường thẳng d.
Lời giải bài tập Toán 9 Bài 13: Mở đầu về đường tròn hay, chi tiết khác: