Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân
Câu hỏi:
Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng:
a) Đường tròn đường kính BC đi qua các điểm H và K;
b) KH < BC.
Trả lời:
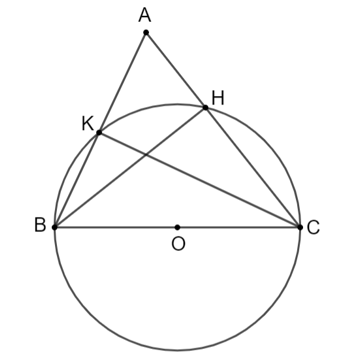
a) Gọi trung điểm của BC là O.
Tam giác vuông BKC có KO là đường trung tuyến KO ứng với cạnh huyền BC nên
KO = OB = OC hay B, K, C thuộc đường tròn tâm O đường kính BC. (1)
Tam giác BHC vuông tại H có HO là đường trung tuyến ứng với cạnh huyền BC nên
HO = BO = OB hay B, H, C thuộc được đường tròn tâm O đường kính BC. (2)
Từ (1) và (2) ta có K, H thuộc đường tròn tâm O đường kính BC.
Vậy đường tròn đường kính BC đi qua các điểm H và K.
b) Đường tròn tâm O có BC là đường kính và KH là dây không qua tâm O.
Do đó KH < BC.