Cho tam giác ABC vuông cân tại A và AB = AC = a (H.4.7a).
Câu hỏi:
Cho tam giác ABC vuông cân tại A và AB = AC = a (H.4.7a).
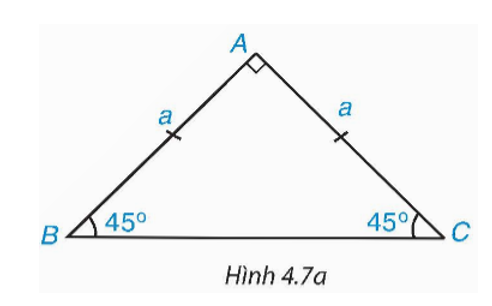
a) Hãy tính BC và các tỉ số Từ đó suy ra sin45°, cos45°.
Trả lời:
Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2 = a2 + a2 = 2a2, suy ra (cm).
∆ABC vuông tại A có AB = AC nên ∆ABC vuông cân tại A nên
a) Ta có: và
Do đó