Dùng MTCT, tìm các góc α (làm tròn đến phút), biết: a) sinα = 0,3782;
Câu hỏi:
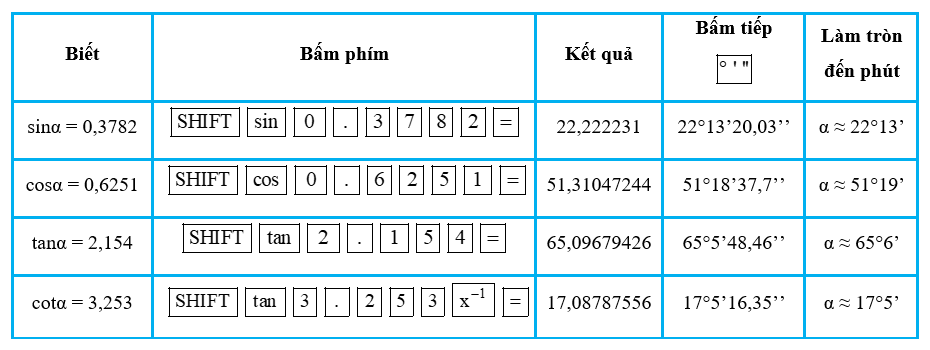
Dùng MTCT, tìm các góc α (làm tròn đến phút), biết:
a) sinα = 0,3782;
b) cosα = 0,6251;
c) tanα = 2,154;
d) cotα = 3,253.
Trả lời:
Câu hỏi:
Dùng MTCT, tìm các góc α (làm tròn đến phút), biết:
a) sinα = 0,3782;
b) cosα = 0,6251;
c) tanα = 2,154;
d) cotα = 3,253.
Trả lời:

Câu 1:
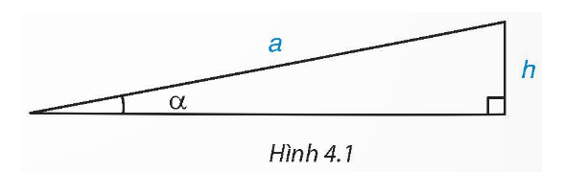
Ta có thể xác định “góc dốc” α của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h không? (H.4.1). (Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn 6°).
Câu 2:
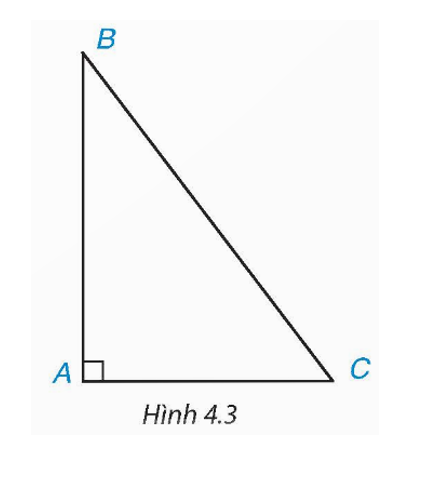
Xét góc C của tam giác ABC vuông tại A (H.4.3). Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Câu 3:
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có Chứng minh rằng:
a) ∆ABC ᔕ ∆A’B’C’;
Câu 5:
Trở lại bài toán ở tình huống mở đầu. Trong một tòa chung cư, biết đoạn dốc vào sảnh tòa nhà dài 4 m, độ cao của đỉnh dốc bằng 0,4 m.
a) Hãy tính góc dốc.
Câu 7:
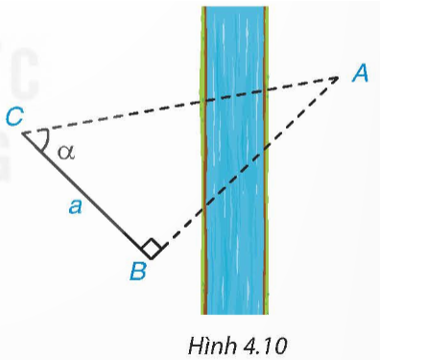
Để tính khoảng cách giữa hai địa điểm A, B không đo trực tiếp được, chẳng hạn A và B là hai địa điểm ở hai bên sông, người ta lấy điểm C về phía bờ sông có chứa B sao cho tam giác ABC vuông tại B. Ở bên bờ sông chứa B, người ta đo được và BC = a (H.4.10). Với các dữ liệu đó, đã tính được khoảng cách AB chưa? Nếu được, hãy tính AB, biết α = 55°, a = 70 m.
Vuông cho rằng: Không thể tính được AB vì trong tam giác vuông ABC, theo định lí Pythagore, phải biết được hai cạnh mới tính được cạnh thứ ba.
Tròn khẳng định: Với các dữ liệu đã biết là có thể tính được khoảng cách AB rồi.
Em hãy cho biết ý kiến của mình.
Câu 8:
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, coossin, tang, cotang của các góc nhọn B và C khi biết:
a) AB = 8 cm, BC = 17 cm;
