Hãy giải thích tại sao sin35° = cos55°, tan35° = cot55°.

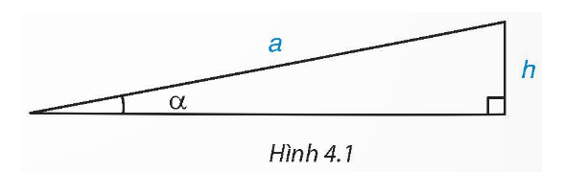
Ta có thể xác định “góc dốc” α của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h không? (H.4.1). (Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn 6°).

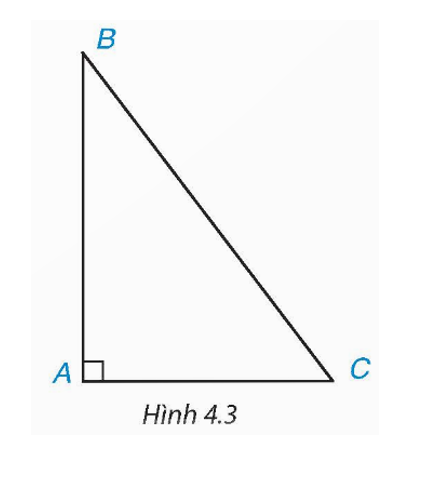
Xét góc C của tam giác ABC vuông tại A (H.4.3). Hãy chỉ ra cạnh đối và cạnh kề của góc C.

Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có $\widehat{B}=\widehat{B^{\text{'}}}=\alpha .$ Chứng minh rằng:

a) ∆ABC ᔕ ∆A’B’C’;

b) $\frac{AC}{BC}=\frac{A^{\text{'}}{C}^{\text{'}}}{B^{\text{'}}{C}^{\text{'}}};\frac{AB}{BC}=\frac{A^{\text{'}}{B}^{\text{'}}}{B^{\text{'}}{C}^{\text{'}}};\frac{AC}{AB}=\frac{A^{\text{'}}{C}^{\text{'}}}{A^{\text{'}}{B}^{\text{'}}};\frac{AB}{AC}=\frac{A^{\text{'}}{B}^{\text{'}}}{A^{\text{'}}{C}^{\text{'}}}.$

Sử dụng MTCT tính các tỉ số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba:

a) sin40°54’;

b) cos52°15’;

c) tan69°36’;

d) cot25°18’.

Dùng MTCT, tìm các góc α (làm tròn đến phút), biết:

a) sinα = 0,3782;

b) cosα = 0,6251;

c) tanα = 2,154;

d) cotα = 3,253.

Trở lại bài toán ở tình huống mở đầu. Trong một tòa chung cư, biết đoạn dốc vào sảnh tòa nhà dài 4 m, độ cao của đỉnh dốc bằng 0,4 m.

a) Hãy tính góc dốc.

b) Hỏi góc đó có đúng tiêu chuẩn của dốc cho người đi xe lăn không?