Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.
Câu hỏi:
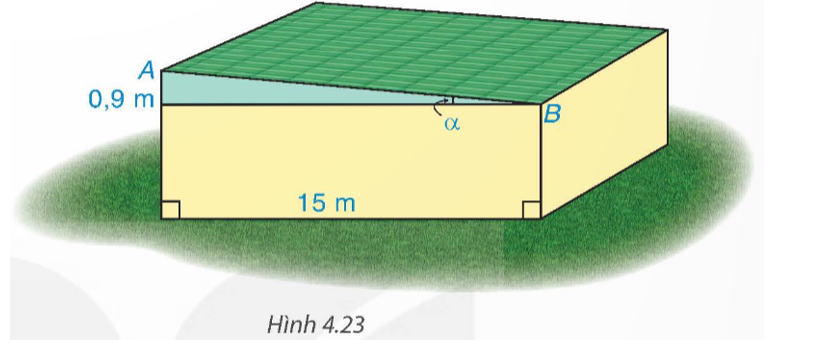
Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23
Trả lời:

Câu hỏi:
Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23

Trả lời:

Câu 1:
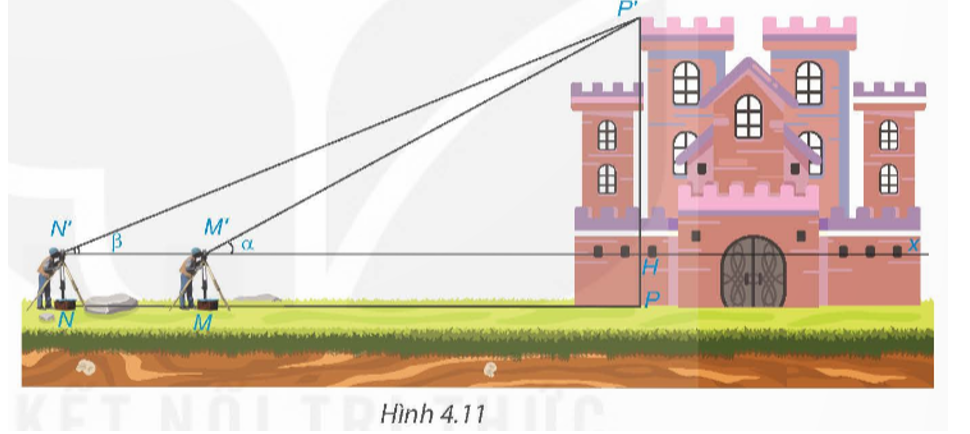
Để đo chiều cao của một toà lâu đài (H.4.11), người ta đặt giác kế thẳng đứng tại điểm M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của toà lâu đài dưới góc nhọn α. Sau đó, đặt giác kế thẳng đứng tại điểm N, NM = 20 m, thì nhìn thấy đỉnh P’ dưới góc nhọn β (β < α). Biết chiều cao giác kế là 1,6 m, hãy tính chiều cao của toà lâu đài.
Câu 2:
Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c (H.4.12).
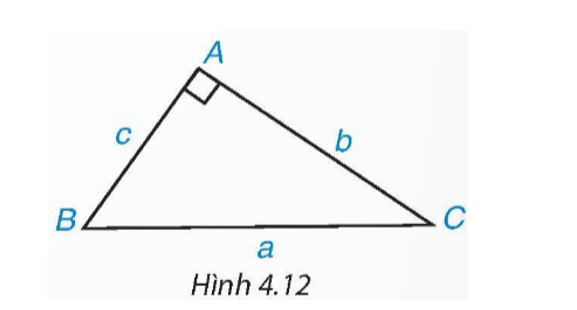
a) Viết các tỉ số lượng giác sin, côsin của góc B và góc C theo độ dài các cạnh của tam giác ABC.
Câu 3:
b) Tính mỗi cạnh góc vuông b và c theo cạnh huyền a và các tỉ số lượng giác trên của góc B và góc C.
Câu 4:
1. Một chiếc thang dài 3 m. Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu mét (làm tròn đến chữ số thập phân thứ hai) để nó tạo được với mặt đất một góc “an toàn” 65° (tức là đảm bảo thang chắc chắn khi sử dụng) (H.4.14)?

Câu 6:
Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm và
a) Kẻ đường cao CE của tam giác ACD. Chứng minh Tính sin của các góc và suy ra AC2 = AE.AD. Từ đó tính AC.
Câu 8:
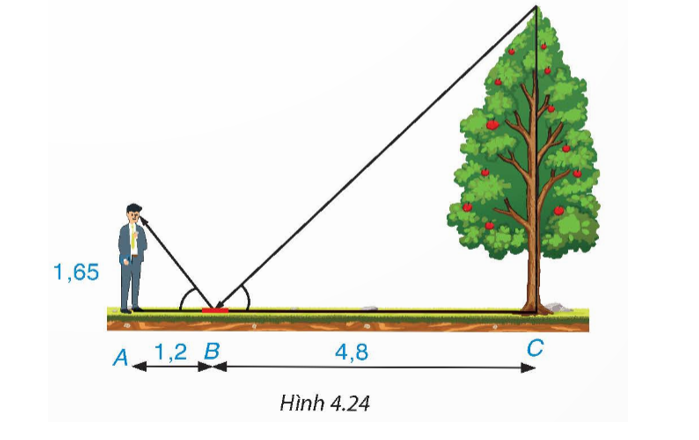
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).