Giải Toán 9 trang 101 Tập 1 Kết nối tri thức
Với Giải Toán 9 trang 101 Tập 1 trong Bài 16: Vị trí tương đối của đường thẳng và đường tròn Toán lớp 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 101.
Giải Toán 9 trang 101 Tập 1 Kết nối tri thức
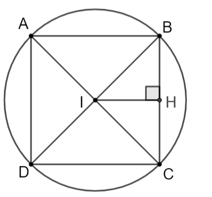
Luyện tập 2 trang 101 Toán 9 Tập 1: Cho một hình vuông có độ dài mỗi cạnh bằng 6 cm và hai đường chéo cắt nhau tại I. Chứng minh rằng đường tròn (I; 3 cm) tiếp xúc với cả bốn cạnh của hình vuông.
Lời giải:
Gọi ABCD là hình vuông có độ dài mỗi cạnh bằng 6 cm; H là chân đường vuông góc kẻ từ I đến BC.
Khi đó H cũng là trung điểm của BC.
Do ABCD là hình vuông nên AC và BD vuông góc.
Tam giác IBC vuông tại I có trung tuyến IH
Suy ra:.
Suy ra đường tròn (I; 3 cm) tiếp xúc với cạnh BC.
Tương tự ta cũng chứng minh được (I; 3 cm) tiếp xúc với 3 cạnh còn lại.
Vậy (I; 3 cm) tiếp xúc với cả bốn cạnh của hình vuông.
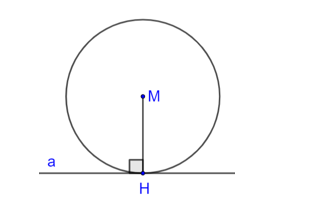
Thực hành trang 101 Toán 9 Tập 1: Cho đường thẳng a và điểm M không thuộc a. Hãy vẽ đường tròn tâm M tiếp xúc với a.
Lời giải:
− Từ điểm M kẻ MH ⊥ a (H ∈ a).
− Vẽ đường tròn tâm M, bán kính MH.
− Từ đó ta vẽ được đường tròn tâm M tiếp xúc với a.
Vận dụng trang 101 Toán 9 Tập 1: Trở lại tình huống mở đầu. Ở đây, ta hiểu đồng xu nằm đè lên một đường thẳng khi đường tròn (hình ảnh của đồng xu) và đường thẳng ấy cắt nhau.
Bằng cách xét vị trí của tâm đồng xu trong một dải nằm giữa hai đường thẳng song song cạnh nhau (cách đều hoặc không cách đều hai đường thẳng đó), hãy chứng minh rằng chỉ xảy ra các trường hợp a và b, không thể xảy ra trường hợp c.
Lời giải:
Đặt tên các đường thẳng a, b, c, d như hình vẽ dưới đây:
Đường kính của đồng xu là: 2 . 1 = 2 (cm).
a) Đường kính của đồng xu là 2 cm và bằng khoảng cách giữa hai đường thẳng song song.
Do đó, đồng xu đè có thể lên một đường thẳng (đồng xu che khuất một phần của đường thẳng).
b) Đồng xu không đè lên đường thẳng a và đường thẳng d.
c) Đồng xu chỉ cắt tối đa một đường thẳng (tức là đè lên một đường thẳng) hoặc đồng xu nằm giữa hai đường thẳng (hai đường thẳng tiếp xúc với đường tròn viền ngoài của đồng xu) hay đồng xu không đè lên đường thẳng nào.
Do đó, không xảy ra trường hợp đồng xu đè lên nhiều hơn một đường thẳng.
Vậy chỉ xảy ra các trường hợp a và b, không thể xảy ra trường hợp c.
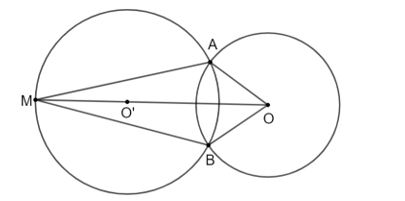
HĐ3 trang 101 Toán 9 Tập 1: Cho điểm M ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau:
− Vẽ đường tròn đường kính MO cắt đường tròn (O) tại A và B;
− Vẽ và chứng tỏ các đường thẳng MA và MB là hai tiếp tuyến của (O).
Lời giải:
• Tam giác OAM có O'A = O'O = O'M (cùng là bán kính của đường tròn (O')) nên tam giác OAM vuông tại A.
Suy ra: AM ⊥ OA tại A hay AM là tiếp tuyến của đường tròn (O').
• Tam giác OBM có O'B = O'O = O'M (cùng là bán kính của đường tròn (O')) nên tam giác OAM vuông tại B.
Suy ra: MB ⊥ OB tại B hay MB là tiếp tuyến của đường tròn (O').
Lời giải bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn hay khác: