Giải Toán 9 trang 80 Tập 1 Kết nối tri thức

---

Với Giải Toán 9 trang 80 Tập 1 trong Luyện tập chung Toán 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 dễ dàng làm bài tập Toán 9 trang 80.

Giải Toán 9 trang 80 Tập 1 Kết nối tri thức

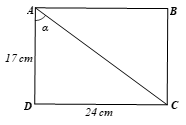
Bài 4.14 trang 80 Toán 9 Tập 1: Một cuốn sách khổ 17 × 24 cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi α là góc giữa đường chéo và cạnh 17 cm. Tính sinα, cosα (làm tròn đến chữ số thập phân thứ hai) và tính số đo α (làm tròn đến độ).

Lời giải:

Ta mô tả cuốn sách khổ 17 × 24 cm như hình vẽ sau:

Xét ∆ACD vuông tại D, theo định lí Pythagore, ta có:

AC² = AD² + DC² = 17² + 24² = 865. Suy ra $AC=\sqrt{865}\text{ cm}$ (vì AC > 0).

Theo định nghĩa tỉ số lượng giác sin và cos, ta có:

$\sin \alpha =\sin \widehat{CAD}=\frac{CD}{AC}=\frac{24}{\sqrt{865}}\approx \mathrm{0,82};$

$\cos \alpha =\cos \widehat{CAD}=\frac{AD}{AC}=\frac{17}{\sqrt{865}}\approx \mathrm{0,58.}$

Suy ra α ≈ 55°.

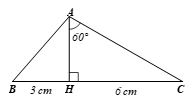
Bài 4.15 trang 80 Toán 9 Tập 1: Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết HB = 3 cm, HC = 6 cm, $\widehat{HAC}=60°.$ Hãy tính độ dài các cạnh (làm tròn đến cm), số đo các góc của tam giác ABC (làm tròn đến độ).

Lời giải:

– Ta có: BC = BH + HC = 3 + 6 = 9 cm.

Xét ∆AHC vuông tại H, ta có:

⦁ $\sin \widehat{HAC}=\frac{CH}{AC}$

Suy ra $AC=\frac{CH}{\sin \widehat{HAC}}=\frac{6}{\sin 60°}=\frac{6}{\frac{\sqrt{3}}{2}}=\frac{12}{\sqrt{3}}=\frac{12\sqrt{3}}{3}=4\sqrt{3}\text{ (cm).}$

⦁ $AH=AC\cdot \cos \widehat{HAC}=4\sqrt{3}\cdot \cos 60°=4\sqrt{3}\cdot \frac{1}{2}=2\sqrt{3}.$

Xét ∆AHB vuông tại H, theo định lý Pythagore ta có:

$A{B}^2=A{H}^2+H{B}^2={\left(2\sqrt{3}\right)}^2+3^2=21$

Suy ra $AB=\sqrt{21}=\mathrm{4,582575695...}\text{ cm}\approx 5\text{ cm.}$

– Ta có: $\widehat{HAC}+\widehat{HCA}=90°$(tổng hai góc nhọn của ∆AHC vuông tại H).

Suy ra $\widehat{HCA}=90°-\widehat{HAC}=90°-60°=30°.$ Hay $\widehat{BCA}=30°.$

Xét ∆AHB vuông tại H, ta có:

$\tan \widehat{HBA}=\frac{AH}{HB}=\frac{2\sqrt{3}}{3},$ suy ra $\widehat{HBA}\approx 49°.$

Xét ∆ABC, ta có: $\widehat{BAC}+\widehat{ACB}+\widehat{ABC}=180°$ (định lý tổng ba góc trong tam giác)

Suy ra $\widehat{BAC}=180°-\widehat{CAB}-\widehat{CBA}\approx 180°-30°-49°=101°.$

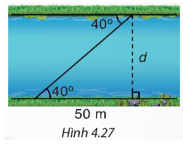
Bài 4.16 trang 80 Toán 9 Tập 1: Tìm chiều rộng d của dòng sông trong Hình 4.27 (làm tròn đến m).

Lời giải:

Ta có: $\tan 40°=\frac{d}{50}$ suy ra d = 50.tan40° ≈ 42 (m).

Vậy chiều rộng của dòng sông là khoảng 42 m.

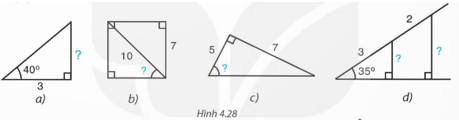
Bài 4.17 trang 80 Toán 9 Tập 1: Tính các số liệu còn thiếu (dấu "?") ở Hình 4.28 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.

Lời giải:

a) Gọi độ dài cạnh cần tìm là x.

Ta có: $\tan 40°=\frac{x}{3}$ suy ra x = 3.tan40° ≈ 2,5.

b) Gọi số đo góc cần tìm là α.

Vì tứ giác đã cho có 3 góc vuông nên là hình chữ nhật. Do đó hai cạnh đối nhau có độ dài bằng nhau.

Ta có: $\sin \alpha =\frac{7}{10}=\mathrm{0,7}$ suy ra α ≈ 44°.

c) Gọi số đo góc cần tìm là β.

Ta có: $\tan \alpha =\frac{7}{5}$ suy ra β ≈ 54°.

d) Gọi độ dài cạnh góc vuông nhỏ và cạnh góc vuông lớn lần lượt là a, b.

Ta có:

⦁ $\sin 35°=\frac{a}{3},$ suy ra a = 3.sin35° ≈ 1,7.

⦁ $\sin 35°=\frac{b}{5},$ suy ra b = 5.sin35° ≈ 2,9.

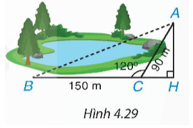
Bài 4.18 trang 80 Toán 9 Tập 1: Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90 m, CB = 150 m và $\widehat{ACB}=120°$ (H.4.29). Hãy tính AB giúp bạn.

Lời giải:

Ta có: $\widehat{BCA}+\widehat{ACH}=180°$(hai góc kề bù)

Suy ra $\widehat{ACH}=180°-\widehat{ACB}=180°-120°=60°.$

Xét ∆AHC vuông tại H, ta có:

⦁ $AH=AC\cdot \sin \widehat{ACH}=90\cdot \sin 60°=90\cdot \frac{\sqrt{3}}{2}=45\sqrt{3}\text{ (m).}$

⦁c$CH=AC\cdot \cos \widehat{ACH}=90\cdot \cos 60°=90\cdot \frac{1}{2}=45\text{ (m).}$

Ta có: BH = BC + CH = 150 + 45 = 195 (m).

Xét ∆AHB vuông tại H, theo định lý Pythagore ta có:

$A{B}^2=A{H}^2+H{B}^2={\left(45\sqrt{3}\right)}^2+{195}^2=44100$

Suy ra $AB=\sqrt{44100}=210\text{ (m).}$

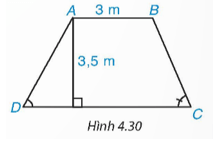
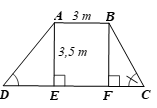
Bài 4.19 trang 80 Toán 9 Tập 1: Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30). Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là tanD = 1,25. Độ dốc của sườn BC, tức là tanC = 1,5. Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).

Lời giải:

Kẻ AE ⊥ CD, BF ⊥ CD. Khi đó AE // BF.

Vì ABCD là hình thang nên AB // CD, do đó suy ra AB // EF.

Xét tứ giác ABFE có: AE // BF và AB // EF nên là hình bình hành.

Lại có $\widehat{E}=90°,$ nên hình bình hành ABFE là hình chữ nhật.

Suy ra EF = AB = 3 m.

Xét ∆ADE vuông tại E, ta có:

$\tan D=\frac{AE}{DE},$ suy ra $DE=\frac{AE}{\tan D}=\frac{\mathrm{3,5}}{\mathrm{1,25}}=\mathrm{2,8}\text{ (m).}$

Vì ABFE là hình chữ nhật nên BF = AE = 3,5 m.

Xét ∆BCF vuông tại F, ta có:

$\tan C=\frac{BF}{FC},$ suy ra $FC=\frac{BF}{\tan C}=\frac{\mathrm{3,5}}{\mathrm{1,5}}=\frac{7}{3}\text{ (m).}$

Ta có: $DC=DE+EF+FC=\mathrm{2,8}+3+\frac{7}{3}=\frac{122}{15}=\text{8,1}\left(3\right)\text{ (m)}\approx 81\text{ (dm).}$

Xét ∆ADE vuông tại E, theo định lí Pythagore, ta có:

AD² = AE² + DE² = 3,5² + 2,8² = 20,09.

Suy ra $AD=\sqrt{\mathrm{20,09}}\approx \mathrm{4,482186966...}\text{ (m)}\approx \text{45 (dm).}$

Xét ∆BCF vuông tại F, theo định lí Pythagore, ta có:

$B{C}^2=B{F}^2+C{F}^2={\mathrm{3,5}}^2+{\left(\frac{7}{3}\right)}^2=\frac{637}{36}.$

Suy ra $BC=\sqrt{\frac{637}{36}}=\mathrm{4,206476388...}\text{ (m)}\approx 42\text{ (dm).}$

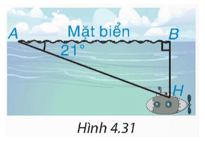
Bài 4.20 trang 80 Toán 9 Tập 1: Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước biển một góc 21° để lặn xuống (H.4.31).

a) Khi tàu chuyển động theo hướng đó và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước biển? (làm tròn đến m).

b) Giả sử tốc độ của tàu là 9 km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200 m (tức là cách mặt nước biển 200 m)?

Lời giải:

a) Tàu chuyển động theo đường thẳng tạo với mặt nước biển một góc 21° và đi được 200 m tức là AH = 200 m. Độ sâu của tàu so với mặt nước biển là BH.

Xét ∆ABH vuông tại B, ta có:

$BH=AH\cdot \sin \widehat{BAH}=200\cdot \sin 21°\approx 72\text{ (m).}$

b) Tàu ở độ sâu 200 m tức là BH = 200 m. Quãng đường tàu đi đến độ sâu 200 m là AH.

 

Xét ∆ABH vuông tại B, ta có:

$\sin \widehat{BAH}=\frac{BH}{AH},$ suy ra $AH=\frac{BH}{\sin 21°}=\frac{200}{\sin 21°}\approx 558\text{ (m)}=\mathrm{0,558}\text{ (km).}$

Thời gian tàu chạy đạt độ sâu 200 m là: $\frac{\mathrm{0,558}}{9}=\mathrm{0,062}$(giờ).