Giải Toán 9 trang 90 Tập 1 Kết nối tri thức

---

Với Giải Toán 9 trang 90 Tập 1 trong Bài 14: Cung và dây của một đường tròn Toán lớp 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 90.

Giải Toán 9 trang 90 Tập 1 Kết nối tri thức

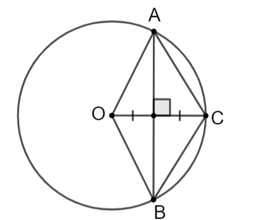
Luyện tập 2 trang 90 Toán 9 Tập 1: Cho điểm C nằm trên đường tròn (O). Đường trung trực của đoạn OC cắt (O) tại A. Tính số đo của các cung $\stackrel{⏜}{ACB}$  và $\stackrel{⏜}{ABC}.$

Lời giải:

Vì AB là đường trung trực của AB của OC nên AC = OA (tính chất đường trung trực).

Mà OA = OC = R nên AC = OA = OC.

Nên ΔACO là tam giác đều.

Do đó: $\widehat{ACO}=60°$  (tính chất của tam giác đều)

Suy ra $sđ\stackrel{⏜}{AC}=60°$ .

Tương tự ta có: $sđ\stackrel{⏜}{BC}=60°$ .

Suy ra: $sđ\stackrel{⏜}{ACB}=sđ\stackrel{⏜}{AC}+sđ\stackrel{⏜}{BC}=60°+60°=120°.$

Ta có $\stackrel{⏜}{ABC}$  là cung lớn có chung hai mút A, C với cung nhỏ $\stackrel{⏜}{AC}.$

Do đó $sđ\stackrel{⏜}{ABC}=360°-sđ\stackrel{⏜}{AC}=360°-60°=300°.$

Vậy $sđ\stackrel{⏜}{ACB}=120°$  và $sđ\stackrel{⏜}{ABC}=300°.$

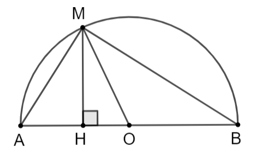
Bài 5.5 trang 90 Toán 9 Tập 1: >Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó. Chứng minh rằng khoảng cách từ M đến AB không lớn hơn $\frac{AB}{2}.$

Lời giải:

Gọi H là hình chiếu của M trên AB.

Khi đó khoảng cách từ M đến AB bằng độ dài đoạn MH.

Xét tam giác MHO vuông tại H có: MH ≤ MO.

Lại có $OM=\frac{AB}{2}$  (do AB là đường kính, OM là bán kính của đường tròn (O)).

Vậy $MH\le \frac{AB}{2}.$

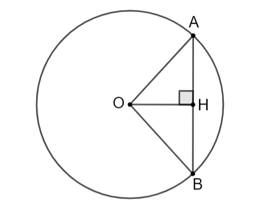
Bài 5.6 trang 90 Toán 9 Tập 1: Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm.

a) Tính khoảng cách từ O đến đường thẳng AB.

b) Tính tan α nếu góc ở tâm chắn cung AB bằng 2α.

Lời giải:

a) Gọi H là trung điểm của AB.

Suy ra $AH=\frac{AB}{2}=\frac{6}{2}=3\text{\hspace{0.17em}\hspace{0.17em}(cm)}.$

Xét ∆OAH và ∆OBH có:

OA = OB = R

Cạnh OH chung

HA = HB (do H là trung điểm của AB)

Do đó ∆OAH = ∆OBH (c.c.c).

Suy ra $\widehat{OHA}=\widehat{OHB}$  (hai góc tương ứng)

Mà $\widehat{OHA}$  và $\widehat{OHB}$  là hai góc bù nhau nên $\widehat{OHA}+\widehat{OHB}=180°$  hay $2\widehat{OHB}=180°$

Suy ra $\widehat{OHA}=\widehat{OHB}=90°$  nên OH ⊥ AB.

Do đó khoảng cách từ O đến đường thẳng AB bằng độ dài đoạn OH.

Xét tam giác OAH vuông tại H có:

AH² + OH² = OA² (định lý Pythagore)

Hay OH² = OA² − AH² = 5² − 3² = 16.

Nên OH = 4 cm.

Vậy khoảng cách từ O đến đường thẳng AB bằng 4 cm.

b) Theo giả thiết, góc ở tâm chắn cung AB là $\widehat{AOB}=2\alpha$ .

Từ câu a) ∆OAH = ∆OBH suy ra $\widehat{HOA}=\widehat{HOB}$  (hai góc tương ứng).

Lại có: $\widehat{HOA}+\widehat{HOB}=\widehat{AOB}$  nên $2\widehat{HOA}=2\alpha$  hay $\widehat{HOA}=\alpha .$

Suy ra $\tan \alpha =\frac{AH}{OH}=\frac{3}{4}.$

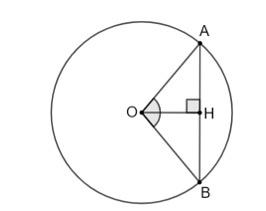
Bài 5.7 trang 90 Toán 9 Tập 1: Tâm O của một đường tròn cách dây AB của nó một khoảng 3 cm. Tính bán kính của đường tròn (O), biết rằng dây cung nhỏ AB có số đo bằng 100° (làm tròn kết quả đến hàng phần mười).

Lời giải:

Gọi H là trung điểm của AB.

Theo giả thiết, góc ở tâm chắn cung AB là $\widehat{AOB}=100°$ .

Xét ∆OAH và ∆OBH có:

OA = OB = R

Cạnh OH chung

HA = HB (do H là trung điểm của AB)

Do đó ∆OAH = ∆OBH (c.c.c).

Suy ra $\widehat{HOA}=\widehat{HOB}$  (hai góc tương ứng).

Lại có: $\widehat{HOA}+\widehat{HOB}=\widehat{AOB}$  nên $2\widehat{HOA}=\widehat{AOB}=100°$  hay $\widehat{HOA}=50°.$

Xét tam giác OAH vuông tại H có: $\cos \widehat{HOA}=\frac{OH}{OA}$ .

Suy ra $OA=\frac{OH}{\cos \widehat{HOA}}=\frac{3}{\cos 50°}\approx 4,7\text{\hspace{0.17em}\hspace{0.17em}(cm)}.$

Vậy bán kính của đường tròn (O) khoảng 4,7 cm.

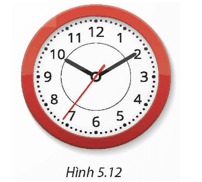
Bài 5.8 trang 90 Toán 9 Tập 1: Trên mặt một chiếc đồng hồ có các vạch chia như Hình 5.12. Hỏi cứ sau mỗi khoảng thời gian 36 phút:

a) Đầu kim phút vạch trên một cung có số đo bằng bao nhiêu độ?

b) Đầu kim giờ vạch trên một cung có số đo bằng bao nhiêu độ?

Lời giải:

a) Cứ 60 phút kim phút chạy hết 1 vòng đồng hồ, tức là vạch trên 1 cung có số đo bằng

360°.

Mỗi phút kim phút vạch trên một cung có số đo là: $\frac{360°}{60}=6°.$

Như vậy sau 36 phút, kim phút vạch trên 1 cung có số đo bằng:

6° . 36 = 216°.

b) Sau 1 giờ, kim giờ vạch trên 1 cung có số đo bằng: $\frac{360°}{12}=30°.$

Mỗi phút kim giờ vạch trên một cung có số đo là: $\frac{30°}{60}=0,5°.$

Như vậy sau 36 phút, kim giờ vạch trên 1 cung có số đo bằng:

0,5° . 36 = 18°.

Lời giải bài tập Toán 9 Bài 14: Cung và dây của một đường tròn hay khác:

• Giải Toán 9 trang 87