Xét bài toán cổ trong tình huống mở đầu. Gọi x là số cam, y là số quýt cần tính (x, y ∈ ℕ*), ta có hệ phương trình bậc nhất hai ẩn sau:
Câu hỏi:
Xét bài toán cổ trong tình huống mở đầu. Gọi x là số cam, y là số quýt cần tính (x, y ∈ ℕ*), ta có hệ phương trình bậc nhất hai ẩn sau:
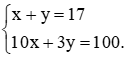
Trong hai cặp số (10; 7) và (7; 10), cặp số nào là nghiệm của hệ phương trình trên? Từ đó cho biết một phương án về số cam và số quýt thỏa mãn yêu cầu của bài toán cổ.
Trả lời:
* Thay x = 10; y = 7 vào hệ phương trình đã cho, ta có:
• x + y = 10 + 7 = 17 nên (10; 7) là nghiệm của phương trình thứ nhất;
• 10x + 3y = 10 . 10 + 3 . 7 = 100 + 21 = 121 ≠ 100 nên (10; 7) không phải là nghiệm của phương trình thứ hai.
Do đó (10; 7) không phải là một nghiệm của hệ phương trình đã cho.
* Thay x = 7; y = 10 vào hệ phương trình đã cho, ta có:
• x + y = 7 + 10 = 17 nên (7; 10) là nghiệm của phương trình thứ nhất;
• 10x + 3y = 10 . 7 + 3 . 10 = 70 + 30 = 100 nên (7; 10) là nghiệm của phương trình thứ hai.
Do đó (7; 10) là nghiệm chung của hai phương trình, nghĩa là (7; 10) là một nghiệm của hệ phương trình đã cho.
Vậy cặp số (7; 10) là nghiệm của hệ phương trình trên; số cam và số quýt thỏa mãn yêu cầu của bài toán cổ là 7 quả quả cam và 10 quả quýt.

