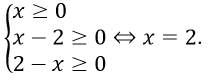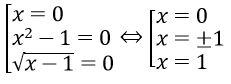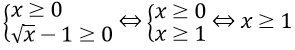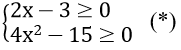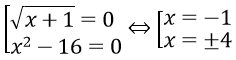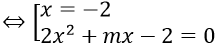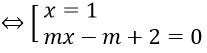Bài tập giải phương trình bằng phương pháp biến đổi tương đương có lời giải - Toán lớp 10

---

Bài tập giải phương trình bằng phương pháp biến đổi tương đương có lời giải

Với Bài tập giải phương trình bằng phương pháp biến đổi tương đương có lời giải Toán lớp 10 tổng hợp 20 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải phương trình bằng phương pháp biến đổi tương đương từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Câu 1. Phương trình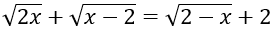có bao nhiêu nghiệm?

A. 0        B. 1        C. 2        D. 3

Câu 2. Phương trình sau có bao nhiêu nghiệm √x = √(-x)

A. 0        B. 1        C. 2        D. vô số

Câu 3. Phương trình x(x²-1)√(x-1) = 0 có bao nhiêu nghiệm ?

A. 0        B. 1        C. 2        D. 3

Câu 4. Phương trình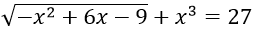có bao nhiêu nghiệm?

A. 0        B. 1        C. 2        D. 3

Câu 5. Số nghiệm của phương trình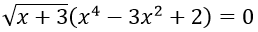là:

A. 1         B. 0        C. 3        D. 5

Câu 6. Phương trình sau có bao nhiêu nghiệm |x| = -x

A. 0        B. 1        C. 2        D. vô số

Câu 7. Phương trình x + √(x-1) = √(1-x) có bao nhiêu nghiệm?

A. 0        B. 1        C. 2        D. 3

Câu 8. Phương trình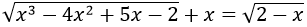có bao nhiêu nghiệm?

A. 0        B. 1        C. 2        D. 3

Câu 9. Phương trình sau có bao nhiêu nghiệm |x - 2| = 2 - x

A. 0        B. 1        C. 2        D. vô số

Câu 10. Phương trình √(-x² + 10x - 25) = 0

A. vô nghiệm

B. vô số nghiệm.

C. mọi x đều là nghiệm

D.có nghiệm duy nhất

Câu 11. Phương trình √(2x+5) = √(-2x-5) có nghiệm là :

A. x = 5/2        B. x = -5/2        C. x = -2/5        D.x = 2/5

Câu 12. Tập nghiệm của phương trình x - √(x-3) = √(3-x) + 3 là :

A. S = ∅        B. S = {3}        C. S = [3; +∞)        D. S = R

Câu 13. Tập nghiệm của phương trình x + √x = √x - 1 là :

A. S = ∅        B. S = {-1}        C. S = {0}        D. S = R

Câu 14. Tập nghiệm của phương trình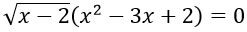 là:

A. S = ∅        B. S = {1}        C. S = {2}        D. S = {1; 2}

Câu 15. Số nghiệm của phương trình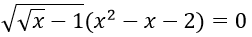 là:

A. 1        B. 0        C. 2        D. 5

Câu 16. Số nghiệm của phương trình √(2x-3) = √(4x²-15) là:

A. 1         B. 0        C. 3        D. 5

Câu 17. Số nghiệm của phương trình |2x+1| = x-1 là:

A. 1        B. 0        C. 3        D. 2

Câu 18. Số nghiệm của phương trình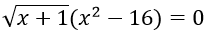là:

A. 1        B. 2        C. 3        D. 0

Câu 19. Tìm giá trị thực của tham số m để cặp phương trình sau tương đương:

2x² + mx - 2 = 0  (1) và 2x³ + (m+4)x² + 2(m-1)x - 4 = 0  (2)

A. m = 2        B. m = 3        C. m = 1/2        D. m = -2

Câu 20. Tìm tất cả các giá trị thực của tham số m để cặp phương trình sau tương đương

mx² - 2(m-1)x + m - 2 = 0  (1) và (m-2)x² - 3x + m² - 15 = 0  (2)

A. m = -5        B. m = -5, m = 4        C. m = 4        D. m = 5

Đáp án và hướng dẫn giải

Câu	1	2	3	4	5	6	7	8	9	10
Đáp án	B	B	B	B	D	D	A	B	D	D

Câu	11	12	13	14	15	16	17	18	19	20
Đáp án	B	B	A	C	C	A	B	B	B	C

Câu 1. Chọn B

Điều kiện:

Thử lại phương trình thấy x = 2 thỏa mãn

Vậy phương trình đã cho có nghiệm duy nhất

Câu 2. Chọn B

Ta có: √x = √(-x) ⇔ x = 0

Câu 3. Chọn B

Điều kiện: x-1 ≥ 0 ⇔ x ≥ 1.

Phương trình tương đương với

Đối chiếu điều kiện, ta được nghiệm của phương trình đã cho là x = 1.

Vậy phương trình đã cho có nghiệm duy nhất.

Câu 4. Chọn B.

Điều kiện: -x² + 6x - 9 ≥ 0 ⇔ -(x-3)² ≥ 0 ⇔ x = 3

Thử lại ta thấy x = 3 thỏa mãn phương trình.

Vậy phương trình đã cho có nghiệm duy nhất.

Câu 5.Chọn D

ĐKXĐ: x ≥ -3

Phương trình tương đương với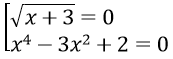

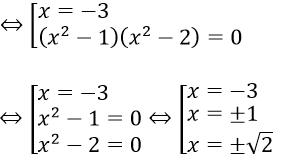
Đối chiếu với điều kiện ta được nghiệm của phương trình là x = -3, x = ±1 và x = ±√2

Câu 6. Chọn D

Ta có: |x| = -x ⇔ x ≤ 0

Câu 7. Chọn A

Điều kiện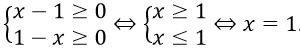

Thử lại x = 1 thì phương trình không thỏa mãn phương trình

Vậy phương trình đã cho vô nghiệm

Câu 8. Chọn B

Điều kiện:

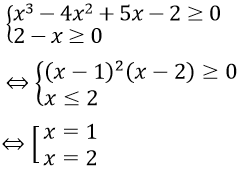
Thay x = 1 và x = 2 vào phương trình thấy chỉ có x = 1 thỏa mãn

Vậy phương trình đã cho có nghiệm duy nhất

Câu 9. Chọn D.

Ta có: |x-2| = 2-x ⇔ x-2 ≤ 0 ⇔ x ≤ 2

Câu 10. Chọn D

Ta có: √(-x² + 10x - 25) = 0 ⇔ -x² + 10x - 25 = 0 ⇔ (x-5)² = 0 ⇔ x = 5

Câu 11. Chọn B

Ta có: √(2x+5) = √(-2x-5) ⇔ 2x + 5 = 0 ⇔ x = -5/2

Câu 12. Chọn B

Ta có: x - √(x-3) = √(3-x) + 3 ⇔ x = 3

Câu 13. Chọn A

Câu 14. Chọn C

Ta có:

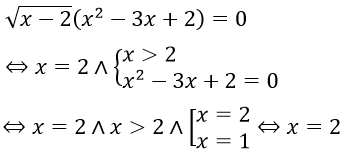
Câu 15. Chọn C

ĐKXĐ:

Với điều kiện đó phương trình tương đương với

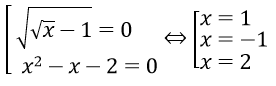
Đối chiếu với điều kiện ta có ngiệm của phương trình là x = 1 và x = 2

Câu 16. Chọn A

ĐKXĐ:

Với điều kiện (*) phương trình tương đương với

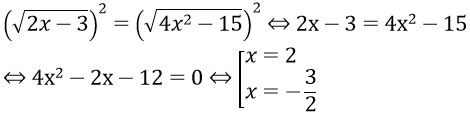
Thay vào điều kiện (*) ta thấy chỉ có x = 2 thỏa mãn

Vậy phương trình có nghiệm duy nhất x = 2

Câu 17. Chọn B

Ta có |2x+1| = x-1 ⇒ (2x+1)² = (x-1)²

⇒ 4x² + 4x + 1 = x² - 2x + 1 ⇔ 3x² + 6x = 0

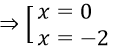
Thử vào phương trình ta thấy không có giá trị nào thỏa mãn

Vậy phương trình vô nghiệm.

Câu 18. Chọn B

ĐKXĐ: x ≥ -1

Phương trình tương đương với

Đối chiếu với điều kiện ta được nghiệm của phương trình là x = -1 và x = 4

Câu 19. Chọn B

Ta có (2)⇔ (x + 2)(2x² + mx - 2) = 0

Do hai phương trình tương đương nên x=-2 cũng là nghiệm của phương trình (1)

Thay x = -2 vào (1), ta được 2(-2)² + m(-2) - 2 = 0 ⇔ m = 3

Với m = 3, ta có

(1) trở thành 2x² + 3x - 2 = 0 ⇔ x = -2 hoặc x = 1/2

(2) trở thành 2x³ + 7x² + 4x - 4 = 0 ⇔ (x+2)²(2x+1) = 0 ⇔ x = -2 hoặc x = 1/2

Câu 20. Chọn C

Ta có (1) ⇔ (x - 1)(mx - m + 2) = 0

Do hai phương trình tương đương nên x=1 cũng là nghiệm của phương trình (2)

Thay x = 1 vào (2), ta được (m - 2) - 3 + m² - 15 = 0 ⇔ m² + m - 20 = 0

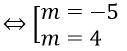
Với m = -5, ta có

+ (1) trở thành -5x² + 12x - 7 = 0 ⇔ x = 7/5 hoặc x = 1

+ (2) trở thành -7x² - 3x + 10 = 0 ⇔ x = -10/7 hoặc x = 1

Suy ra hai phương trình không tương đương

Với m = 4, ta có

+ (1) trở thành 4x² - 6x + 2 = 0 ⇔ x = 1/2 hoặc x = 1

+ (2) trở thành 2x² - 3x + 1 = 0 ⇔ x = 1/2 hoặc x = 1

Vậy m = 4 thì phương trình tương đương