Cách giải và biện luận phương trình bậc nhất cực hay, chi tiết - Toán lớp 10

---

Cách giải và biện luận phương trình bậc nhất cực hay, chi tiết

Với Cách giải và biện luận phương trình bậc nhất cực hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Cách giải và biện luận phương trình bậc nhất từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Lý thuyết & Phương pháp giải

Cách giải và biện luận phương trình dạng ax+b=0 được tóm tắt trong bảng sau

ax + b = 0  (1)
Hệ số		Kết luận
a ≠ 0		(1) có nghiệm duy nhất x = -b/a
a = 0	b ≠ 0	(1) vô nghiệm
	b = 0	(1) nghiệm đúng với mọi x

Khi a ≠ 0 phương trình ax + b = 0 được gọi là phương trình bậc nhất một ẩn

Ví dụ minh họa

Bài 1: Cho phương trình (m² - 7m + 6)x + m² - 1 = 0

a. Giải phương trình khi m = 0

b. Biện luận theo m số nghiệm của phương trình

Hướng dẫn:

a. Với m = 0 phương trình trở thành 6x - 1 = 0 ⇔ x = 1/6

Phương trình có nghiệm duy nhất x = 1/6

b. Ta có (m² - 7m + 6)x + m² - 1 = 0 ⇔ (m-1)(m-6)x + (m-1)(m+1) = 0

Nếu (m-1)(m-6) ≠ 0 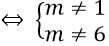thì phương trình có nghiệm duy nhất x = -(m+1)/(m-6)

Nếu m = 1 phương trình trở thành 0 = 0. Khi đó phương trình có vô số nghiệm.

Nếu m = 6 thì phương trình trở thành 35 = 0 (Vô lí). Khi đó phương trình vô nghiệm.

Bài 2: Tìm tất cả các giá trị thực của tham số m để phương trình (2m - 4)x = m - 2 có nghiệm duy nhất.

Hướng dẫn:

Phương trình đã cho có nghiệm duy nhất khi 2m - 4 ≠ 0 ⇔ m ≠ 2

Bài 3: Tìm tất cả các giá trị thực của tham số m để phương trình (m² - 5m + 6)x = m² - 2m vô nghiệm.

Hướng dẫn:

Phương trình đã cho vô nghiệm khi

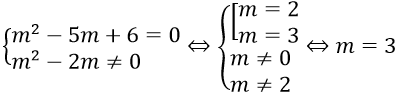
Bài 4: Tìm tất cả các giá trị thực của tham số m để phương trình (m² - 1)x = m - 1 có nghiệm đúng với mọi x thuộc R.

Hướng dẫn:

Phương trình đã cho nghiệm đúng với ∀x ∈ R hay phương trình có vô số nghiệm khi

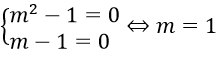
Bài 5: Cho phương trình m²x + 6 = 4x + 3m. Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm.

Hướng dẫn:

Phương trình viết lại (m² - 4)x = 3m - 6.

Phương trình đã cho vô nghiệm khi

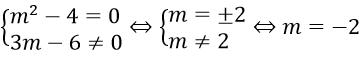
Do đó, phương trình đã cho có nghiệm khi m ≠ -2

Bài 6: Cho hai hàm số y = (m + 1)²x - 2 và y = (3m + 7)x + m. Tìm tất cả các giá trị của tham số m để đồ thị hai hàm số đã cho cắt nhau.

Hướng dẫn:

Đồ thị hai hàm số cắt nhau khi và chỉ khi phương trình

(m + 1)²x - 2 = (3m + 7)x + m có nghiệm duy nhất

⇔ (m² - m - 6)x = 2 + m có nghiệm duy nhất

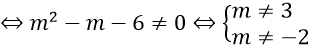
Bài 7: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 10] để phương trình (m² - 9)x = 3m(m - 3) có nghiệm duy nhất ?

Hướng dẫn:

Phương trình đã cho có nghiệm duy nhất khi m²-9 ≠ 0 ⇔ m ≠ ±3

Vì m ∈ Z, m ∈ [-10; 10] nên

m ∈ {-10; -9; -8;...; -4; -2; -1; 0; 1; 2; 4;...; 10}

Vậy 19 giá trị của tham số m thỏa mãn yêu cầu bài toán.