Bài tập tổng hợp Chương 2: Hàm số bậc nhất và bậc hai chọn lọc, có lời giải - Toán lớp 10

---

Bài tập tổng hợp Chương 2: Hàm số bậc nhất và bậc hai chọn lọc, có lời giải

Với Bài tập tổng hợp Chương 2: Hàm số bậc nhất và bậc hai chọn lọc, có lời giải Toán lớp 10 tổng hợp 45 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hàm số bậc nhất và bậc hai từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Câu 1: Cho hàm số: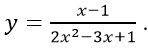Trong các điểm sau đây điểm nào thuộc đồ thị hàm số?

A. (2; 3)        B. (0; 1)        C. (2; 4)        D. (1; 0)

Câu 2: Cho hàm số: y = f(x) = |2x - 3|. Tìm x để f(x) = 3.

A. x = 3        B. x = 3 hay x = 0

C. x = ±3        D. Một kết quả khác

Câu 3: Cho hàm số: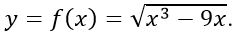Kết quả nào sau đây đúng?

A. f(0) = 2; f(-3) = -4.

B. f(2): không xác định, f(-3) = -5.

C. f(-1) = √8; f(2): không xác định.

D. Tất cả các câu trên đều đúng.

Câu 4: Tập xác định của hàm số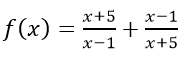là:

A. D = R        B. D = R\{1}        C. D = R\{-5}        D. D = R\{1; -5}

Câu 5: Tập xác định của hàm số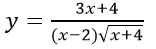

A. D = R\{2}        B. D = (-4;+∞)\{2}

C. D = [-4; +∞)\{2}        D. D = ∅

Câu 6: Tập xác định của hàm số: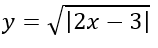

A. [3/2;+∞)        B. (3/2;+∞)        C. (-∞; 3/2)        D. D = R

Câu 7: Hàm số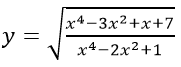có tập xác định là:

A. [-2; -1) ∪ (1;3]        B. [-2; -1] ∪ [1;3)

C. R\{-1;1}        D. (-2;-1) ∪ (-1;1) ∪ (1;3)

Câu 8: Cho hàm số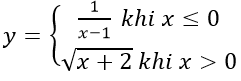. Tập xác định của hàm số là tập hợp nào đây?

A. [-2; +∞)        B. R\{1}

C. R        D. {x ∈ R|x ≠ 1,x ≥ -2}

Câu 9: Hàm số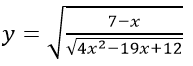có tập xác định là:

A.(-∞; 3/4] ∪ [4;7]        B.(-∞; 3/4) ∪ [4;7)

C.(-∞; 3/4] ∪ (4;7)        D.(-∞; 3/4) ∪ (4;7]

Câu 10: Với giá trị nào của m thì hàm số y = (2 - m)x + 5m là hàm số bậc nhất:

A. m < 2        B. m > 2        C. m ≠ 2        D. m = 2

Câu 11: Xác định m để ba đường thẳng y = 1 - 2x, y = x - 8 và y = (3 + 2m)x - 5 đồng quy

A. m = -1        B. m = 1/2        C. m = 1        D. m = -3/2

Câu 12: Cho đồ thị hàm số y = f(x) như hình vẽ

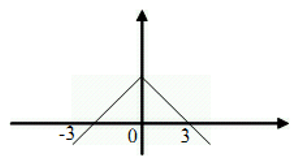
Kết luận nào trong các kết luận sau là đúng:

A. Đồng biến trên R        B. Hàm số chẵn

C. Hàm số lẻ        D. Cả ba đáp án đếu sai

Câu 13: Với những giá trị nào của m thì hàm số y = -x³ + 3(m² - 1)x² + 3x là hàm số lẻ:

A. m = 1        B. m = -1        C. m = ±1        D. Kết quả khác.

Câu 14: Đồ thị hàm số y = ax + b đi qua hai điểm A(0; -3),B(-1; -5) thì a và b bằng:

A. a = -2; b = 3        B. a = 2, b = 3

C. a = 2; b = -3        D. a = 1; b = 4

Câu 15: Hàm số y = -x² + 2(m - 1)x + 3 nghịch biến trên (1; +∞) khi giá trị m thỏa mãn:

A. m ≤ 0        B. m > 0        C. m ≤ 2        D. 0 < m ≤ 2

Đáp án và hướng dẫn giải

1-D	2-B	3-C	4-D	5-B	6-D	7-C	8-C
9-D	10-C	11-B	12-B	13-C	14-C	15-C

Câu 2: Đáp án B

Ta có: f(x) = 3 ⇒ |2x - 3| = 3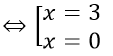

Câu 7: Đáp án C

Ta có x⁴ - 3x² + x + 7 = x⁴ - 4x² + 4 + x² + x + 3

= (x² - 2)² + x² + x + 3 > 0

Do đó, ĐKXĐ: x² - 1 ≠ 0 ⇔ x ≠ ±1

Câu 8: Đáp án C

Với x ≤ 0 thì y = 1/(x-1) ta có x - 1 ≤ -1 < 0 nên x – 1 ≠ 0

Với x > 0 thì y = √(x + 2) ta có x + 2 > 2 > 0

Do đó tập xác định của hàm số là R.

Câu 9: Đáp án D

Điều kiện:

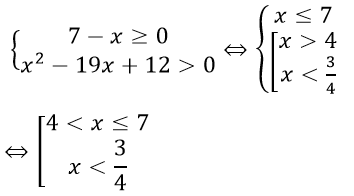
Câu 11: Đáp án D

Tọa độ giao điểm của đường thẳng y = 1 - 2x và y = x - 8 là nghiệm của hệ phương trình:

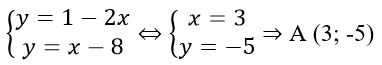
Do 3 đường thẳng đồng quy nên đường thẳng y = (3 + 2m)x - 5 đi qua điểm A (3; -5)

⇒ -5 = (3 + 2m).3 - 5 ⇒ m = -3/2

Câu 12: Đáp án B

Đồ thị của hàm số chẵn đối xứng qua trục tung.

Câu 13: Đáp án C

Đặt f(x) = -x³ + 3(m² - 1)x² + 3x ⇒ f(-x) = x³ + 3(m² - 1)x² - 3x

Để hàm số đã cho là hàm số lẻ thì f(x) = -f(-x) ⇔ (m² - 1)x² = 0 ⇔ m = ±1

Câu 15: Đáp án C

Đồ thị hàm số có trục đối xứng là đường x = m - 1. Đồ thị hàm số đã cho có hệ số x² âm nên sẽ đồng biến trên (-∞; m - 1) và nghịch biến trên (m - 1; +∞). Theo đề, cần: m - 1 ≤ 1 ⇔ m ≤ 2.

Câu 16: Đồ thị hàm số y = m²x + m + 1 tạo với các trục tam giác cân khi m bằng:

A. 1        B. -1        C. ±1        D. 0

Câu 17: Tìm m để hàm số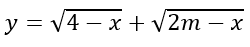có tập xác định là (-∞;4].

A. m ≤ 1        B. m ≥ 4        C. m ≥ 2        D. m ≤ 0

Câu 18: Cho hàm số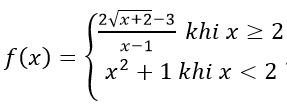Khi đó, f(2) + f(-2) bằng:

A. 8/3        B. 6        C. 4        D. 5/3

Câu 19: Cho hàm số y = f(x) có tập xác định là [-3; 3] và đồ thị của nó được biểu diễn bởi hình bên. Khẳng định nào sau đây là khẳng định đúng?

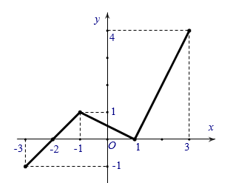
A. Hàm số đồng biến trên khoảng (-3; -1) và (1; 3)

B. Hàm số đồng biến trên khoảng (-3; 1) và (1; 4)

C. Đồ thị cắt trục hoành tại 3 điểm phân biệt

D. Hàm số nghịch biến trên khoảng (-2; 1).

Câu 20: Cho hàm số f(x) = 3x⁴ - 4x² + 3. Trong các mệnh đề sau, mệnh đề nào đúng?

A. y = f(x) là hàm số chẵn

B. y = f(x) là hàm số lẻ

C. y = f(x) là hàm số không có tính chẵn lẻ

D. y = f(x) là hàm số vừa chẵn vừa lẻ

Câu 21: Cho hai hàm số f(x) = x³ - 3x và g(x) = -x³ + x². Khi đó:

A. f(x) và g(x) cùng lẻ

B. f(x) lẻ, g(x) chẵn

C. f(x) chẵn, g(x) lẻ

D. f(x) lẻ, g(x) không chẵn, không lẻ.

Câu 22: Trong các hàm số sau, hàm số nào tăng trên khoảng (-1; 0)?

A. y = x        B. y = 1/x        C. y = |x|        D. y = x²

Câu 23: Xét sự biến thiên của hàm số y = √(x² ). Mệnh đề nào sau đây đúng?

A. Hàm số luôn đồng biến

B. Hàm số đồng biến trên (-∞;0), nghịch biến trên (0; +∞)

C. Hàm số đồng biến trên [0; +∞) , nghịch biến trên (-∞;0)

D. Hàm số đồng biến trên (-∞;2), nghịch biến trên (2; +∞)

Câu 24: Câu nào sau đây đúng?

A. Hàm số y = a²x + b đồng biến khi a > 0 và nghịch biến khi a < 0.

B. Hàm số y = a²x + b đồng biến khi b > 0 và nghịch biến khi b < 0.

C. Với mọi b, hàm số y = -a²xb nghịch biến khi a ≠ 0

D. Hàm số y = a²x + b đồng biến khi a > 0 và nghịch biến khi b < 0

Câu 25: Xét sự biến thiên của hàm số y = 1/x² . Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên (-∞;0), nghịch biến trên (0; +∞)

B. Hàm số đồng biến trên (0; +∞), nghịch biến trên (-∞;0)

C. Hàm số đồng biến trên (-∞;1), nghịch biến trên (1; +∞)

D. Hàm số nghịch biến trên (-∞;0) ∪ (0; +∞)

Câu 26: Hàm số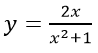có tập giá trị là:

A.[(-1)/2; 1/2]        B.[-1;1]        C.[-2;2]        D.[0;1]

Câu 27: Hàm số y = ax + b. Đâu là khẳng định sai:

A. đồng biến trên R khi a > 0        B. nghịch biến trên R khi a < 0

C. đồng biến trên R khi a = 0        D. không nghịch biến trên R khi a = 0

Câu 28: Cho parabol (P): y = ax² + bx + c. Điều kiện để (P) cắt không cắt trục hoành là:

A. b² - 4ac ≥ 0        B. b² - 4ac > 0

C. b² - 4ac ≤ 0        D. b² - 4ac < 0

Câu 29: Cho hàm số f(x) = 4x³ - 3x² + 2x + 1. Hàm số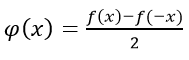có công thức là:

A. φ(x) = 4x³ + 2x        B. φ(x) = 4x³ - 2x

C. φ(x) = -4x³ - 2x        D. φ(x) = -4x³ + 2x

Câu 30: Hàm số y = f(x) thỏa mãn hệ thức 2f(x) + 3f(-x) = 3x + 2, ∀ x. Hàm số f(x) có công thức là:

A. f(x) = -3x + 2/5        B. f(x) = 3x - 2/5

C. f(x) = -3x - 2/5        D. f(x) = 3x + 2/5

Đáp án và hướng dẫn giải

16-A	17-C	18-B	19-A	20-A	21-D	22-D	23-A
24-C	25-A	26-B	27-C	28-D	29-A	30-A

Câu 16: Đáp án A

Để đồ thị hàm số đã cho cắt 2 trục thì m ≠ 0 và không đi qua điểm (0;0)

⇒ m ≠ -1.

Cho x = 0 ⇒ y = m + 1 ⇒ Đồ thị hàm số cắt trục Oy tại điểm (0; m + 1)

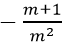
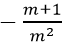
Cho y = 0 ⇒ x =⇒ Đồ thị hàm số cắt trục Ox tại điểm (;0).

Theo yêu cầu bài toán, cần:

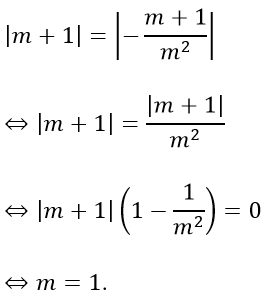
Câu 17: Đáp án C

Tập xác định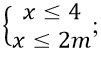theo bài ra D = (-∞; 4]

⇒ 2m ≥ 4 ⇒ m ≥ 2

Câu 20: Đáp án A

TXĐ: R

Ta có: f(-x) = 3(-x)⁴ - 4(-x)² + 3 = 3x⁴ - 4x² + 3 = f(x)

Vậy hàm số là hàm chẵn.

Câu 21: Đáp án D

TXĐ: R

Ta có

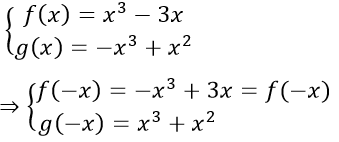
Suy ra f(x) lẻ và g(x) không chẵn không lẻ

Câu 22: Đáp án A

Ta có: y = x = f(x) ⇒ f(0) > f(-1), hàm tăng.

Câu 23: Đáp án B

y = √(x²) = |x|. Đồ thị hàm số các dạng như hình vẽ

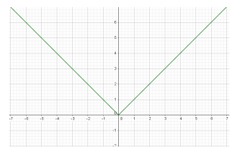
Câu 24: Đáp án C

Hàm số bậc nhất phụ thuộc vào hệ số gắn x

Câu 25: Đáp án A

TXĐ: D = R\{0}

Lấy x₁; x₂ ∈ D, x₁ ≠ x₂, ta có:

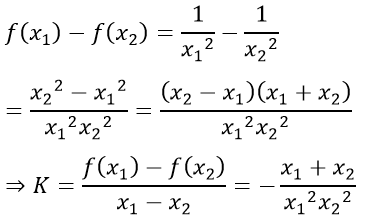
Với x₁; x₂ (-∞;0) ⇒ K > 0

Với x₁; x₂ (0; +∞) ⇒ K < 0

Suy ra hàm số đồng biến trên (-∞;0), nghịch biến trên (0; +∞)

Câu 26: Đáp án B

Ta có: x² + 1 ≥ 2x ≥ -(x² + 1) ⇒ 1 ≥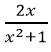≥-1

Câu 28: Đáp án D

Để hàm số không cắt trục hoành thì phương trình ax² + bx + c = 0 vô nghiệm

⇔ Δ = b² - 4ac < 0

Câu 29: Đáp án A

Ta có: f(x) = 4x³ - 3x² + 2x + 1 ⇒ f(-x) = f(x) = -4x³ - 3x² - 2x + 1

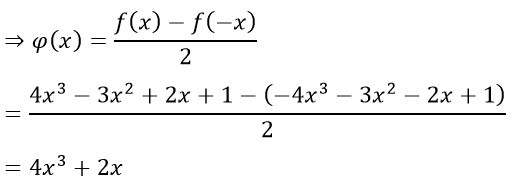
Câu 30: Đáp án A

Ta có: 2f(x) + 3f(-x) = 3x + 2, ∀ x

Thay x bằng –x ta có hệ thức mới là: 2f(-x) + 3f(x) = -3x + 2, ∀ x

Từ đó ta có hệ:

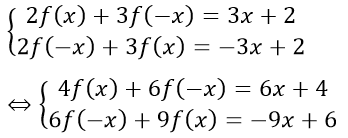
⇒ 5f(x) = -15x + 2 ⇒ f(x) = -3x + 2/5

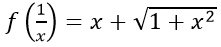
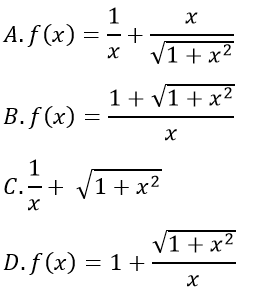
Câu 31: Với x > 0, nếuthì f(x) bằng:

Câu 32: Đường thẳng đi qua điểm A (1; 2) và song song với đường thẳng y = -2x + 3 có phương trình là:

A. y = -2x – 4        B. y = -2x + 4

C. y = -3x + 5        D. y = 2x

Câu 33: Đường thẳng đi qua điểm A (1; 2) và vuông góc với đường thẳng y = - 2x + 3 có phương trình là:

A. 2x + y – 4 = 0        B. x – 2y + 3 = 0

C. x – 2y – 3 = 0        D. 2x – y + 3 = 0

Câu 34: Hàm số y = x + |x + 1| có đồ thị là:

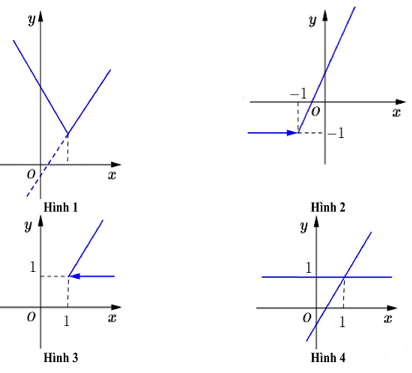
A. Hình 1        B. Hình 2        C. Hình 3        D. Hình 4.

Câu 35: Giá trị của m để hai đường (d₁ ): (m - 1)x + my - 5 = 0,

(d₂ ): mx + (2m - 1)y + 7 = 0 cắt nhau tại một điểm trên trục hoành là:

A. m = 7/12        B. m = 1/2        C. m = 5/12        D. m = 4

Câu 36: Cho parabol (P): y = -3x² + 6x - 1. Khẳng định đúng nhất trong các khẳng định sau là:

A. (P) có đỉnh I(1; 2).        B. (P) có trục đối xứng x = 1.

C. (P) cắt trục tung tại điểm A(0; -1).        D. Cả A, B, C, đều đúng.

Câu 37: Đường thẳng nào trong các đường thẳng sau đây là trục đối xứng của parabol y = -2x² + 5x + 3 ?

A. x = 5/2        B. x = -5/2        C. x = 5/4        D. x = -5/4

Câu 38: Cho hàm số y = f(x) = ax² + bx + c. Biểu thức f(x + 3) - 3f(x + 2) + 3f(x + 1) có giá trị bằng:

A. ax² - bx - c        B. ax² + bx - c

C. ax² - bx + c        D. ax² + bx + c

Câu 39: Giá trị nhỏ nhất của hàm số y = 2x² + x - 3 là:

A. -3        B. -2        C. (-21)/8        D. (-25)/8

Câu 40: Giá trị nhỏ nhất của hàm số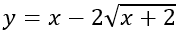là:

A. -4        B. -3        C. -2        D. -1

Câu 41: Phương trình x⁴ - 2x² + 3 - m = 0 có nghiệm khi:

A. m ≥ 3        B. m ≥ -3        C. m ≥ 2        D. m ≥ -2

Câu 42: Phương trình -2x² - 4x + 3 = m có nghiệm khi:

A. m ≤ 5        B. m ≥ 5        C. m < 5        D. m < 5

Câu 43: Phương trình x² - 2|x| - 3 = m có 4 nghiệm phân biệt khi:

A. 0 < m < 4        B. -4 ≤ m ≤ 0

C. 0 ≤ m ≤ 4        D. m ≥ 4

Câu 44: Phương trình |x² - 2x - 3| = m có 2 nghiệm phân biệt khi:

A. m = -4        B. m ≥ -3

C. -4 ≤ m ≤ -3        D. m = - 4 hoặc m > - 3

Câu 45: Cho hai hàm số f(x) đồng biến và g(x) nghịch biến trên khoảng (a; b). Có thể kết luận gì về chiều biến thiên của hàm số y = f(x) + g(x) trên khoảng (a; b) ?

A. đồng biến        B. nghịch biến

C. không đổi        D. không kết luận được

Câu 46: Xác định (P): y = -2x² + bx + c, biết (P) có đỉnh là I(1;3)

A. (P): y = -2x² + 4x + 1        B. (P): y = -2x² + 3x + 1

C. (P): y = -2x² - 4x + 1        D. (P): y = -2x² + 4x - 1

Câu 47: Gọi A (a;b) và B (c; d) là tọa độ giao điểm của (P): y = 2x - x² và Δ: y = 3x - 6. Giá trị của b + d bằng:

A. 7        B. -7        C. -15        D. 15

Câu 48: Phương trình đường thẳng đi qua hai điểm A(5; 2), B(-3; 2) là:

A. y = 5        B. y = -3        C. y = 5x + 2        D. y = 2

Câu 49: Trong mặt phẳng Oxy cho đường thẳng (d) có phương trình y = kx + k² - 3. Tìm k để đường thẳng d đi qua gốc tọa độ:

A. k = √3        B. k = √2

C. k = -√2        D. k = √3 hoặc k = -√3

Câu 50: Phương trình đường thẳng đi qua giao điểm hai đường thẳng y = 2x + 1 và y = 3x - 4 và song song với đường thẳng y = √2.x + 15 là:

A. y = √2.x + 11 - 5√2        B. y = x + 5√2

C. y = √6.x - 5√2        D. y = 4x + √2

Đáp án và hướng dẫn giải

31-B	32-A	33-B	34-B	35-A	36-D	37-C	38-D	39-D	40-B
41-C	42-A	43-A	44-A	45-D	46-A	47-D	48-C	49-D	50-A

Câu 31: Đáp án B

Đặt t = 1/x > 0 với x > 0 ⇒ x = 1/t

Thay vào ta có:

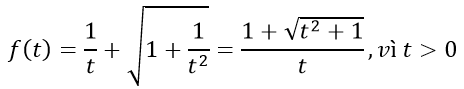
Câu 34: Đáp án B

Xét hàm số

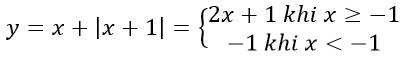
Với x ≥ -1, đồ thị hàm số là đường thẳng y = 2x + 1 .

Với x < -1, đồ thị hàm số là đường thẳng y = -1.

Vậy đồ thị hàm số ở hình 3 thỏa mãn điều kiện trên.

Câu 35: Đáp án A

Gọi M(x; 0) ∈ Ox là giao điểm của d₁,d₂.

Ta có:

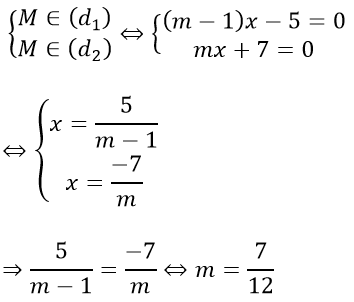
Câu 38: Đáp án D

Ta có: f(x + 3) - 3f(x + 2) + 3f(x + 1)

= a(x + 3)² + b(x + 3) + c - 3[a(x + 2)² + b(x + 2) + c] + 3[a(x + 1)² + b(x + 1) + c]

= ax² + bx + c.

Câu 40 :Đáp án B

y = x - 2√(x + 2) = x + 2 - 2√(x + 2) - 2

Đặt t = √(x+2), t ≥ 0 hàm số trở thành: f(t) = t² - 2t - 2

Ta có:

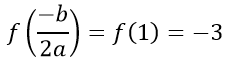
Vậy giá trị nhỏ nhất của hàm số là -3.

Câu 41: Đáp án C

Phương trình x⁴ - 2x² + 3 - m = 0 ⇔ (x² - 1)² = m - 2

Do đó phương trình có nghiệm khi m - 2 ≥ 0 ⇔ m ≥ 2.

Câu 42: Đáp án A

Phương trình -2x² - 4x + 3 = m ⇔ 2x² + 4x + m - 3 = 0     (*)

Phương trình (*) có nghiệm ⇔ Δ' = 2² - 2(m - 3) ≥ 0 ⇔ m ≤ 5.

Câu 43: Đáp án A

Phương trình |x² - 2x - 3| = m

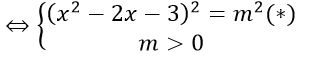
(*) ⇔ (x² - 2x - 3)² - m² = 0

⇔ (x² - 2x - 3 + m)(x² - 2x - 3 - m) = 0

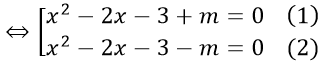
Để phương trình có 4 nghiệm phân biệt thì phương trình (1), (2) có hai nghiệm phân biệt

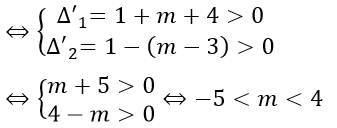
Kết hợp với điều kiện m > 0, ta được 0 < m < 4 là giá trị cần tìm.

Câu 44: Đáp án A

Đặt t = |x| > 0, phương trình x² - 2|x| - 3 = m ⇔ t² - 2t - 3 - m = 0     (*)

Phương trình có hai nghiệm phân biệt ⇔ (*) có nghiệm duy nhất khác 0

⇔ Δ' = 1 + 3 + m = 0 ⇔ m = -4

Với m = -4 thì phương trình có nghiệm duy nhất và khác 0.

Câu 47: Đáp án D

Phương trình hoành độ giao điểm của (P): y = 2x - x² và Δ: y = 3x - 6 là: 2x - x² = 3x - 6 ⇔ x² + x - 6 = 0

Phương trình có hai nghiệm phân biệt, do đó, theo định lí Vi-et ta có:

x₁ + x₂ = -1

⇒ b + d = (3x₁ - 6) + (3x₂ - 6) = 3(x₁ + x₂ ) - 12 = -15