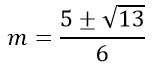Bài tập tổng hợp về hàm số chọn lọc, có lời giải - Toán lớp 10

Bài tập tổng hợp về hàm số chọn lọc, có lời giải

Với Bài tập tổng hợp về hàm số chọn lọc, có lời giải Toán lớp 10 tổng hợp 11 bài tập có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Bài 1. Tìm tập xác định của các hàm số sau:

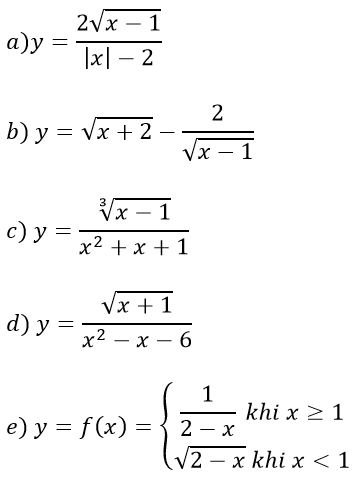
Bài 2: Tìm giá trị của tham số m để:

a) Hàm số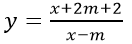xác định trên (-1; 0)

b) Hàm số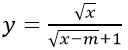có tập xác định là [0; +∞)

Bài 3: Tìm giá trị của tham số m để:

a) Hàm số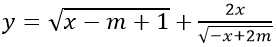xác định trên (-1; 3)

b) Hàm số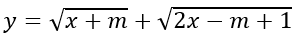xác định trên (0;+∞)

Bài 4: Xét tính chẵn, lẻ của các hàm số sau:

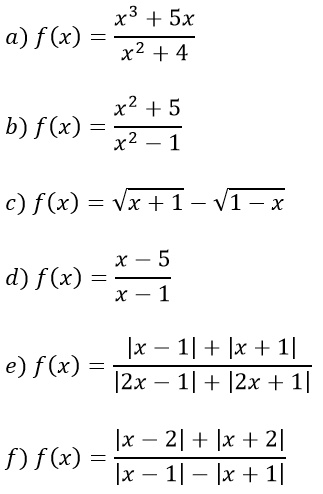
Bài 5: Cho hàm số y = f(x), y = g(x) có cùng tập xác định D. Chứng minh rằng

a) Nếu hai hàm số trên lẻ thì hàm số y = f(x) + g(x) là hàm số lẻ

b) Nếu hai hàm số trên một chẵn một lẻ thì hàm số y = f(x).g(x) là hàm số lẻ

Bài 6:

a) Tìm m để đồ thị hàm số sau nhận gốc tọa độ O làm tâm đối xứng

y = x³ - (m² - 9)x² + (m + 3)x + m - 3.

b) Tìm m để đồ thị hàm số sau nhận trục tung làm trục đối xứng

y = x⁴ - (m² - 3x + 2)x³ + m² - 1

Bài 7: Xét sự biến thiên của các hàm số sau:

a) y = 4 – 3x

b) y = x² + 4x - 5

c) y = 2/(x-2) trên (-∞; 2) và (2; +∞)

d) y = x/(x-1) trên (-∞; 1)

Bài 8: Chứng minh rằng hàm số y = x³ + x đồng biến trên R.

Áp dụng tìm số nghiệm của phương trình sau x³ - x =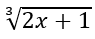+ 1

Bài 9: Cho hàm số y = √(x-1) + x² - 2x

a) Xét sự biến thiên của hàm số đã cho trên [1; +∞)

b) Tìm giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn [2; 5]

Bài 10: Tìm các điểm cố định mà đồ thị hàm số sau luôn đi qua với mọi m.

a) y = x³ + 2(m-1)x² + (m² - 4m + 1)x - 2(m² + 1)

b)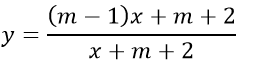

Bài 11: Cho hàm số f(x) = 2x⁴ + (m-1)x³ + (m² - 1)x² + 2(m² - 3m + 2)x - 3.

Tìm m để điểm M(1;0) thuộc đồ thị hàm số đã cho.

Đáp án và hướng dẫn giải

Bài 1:

a) ĐKXĐ: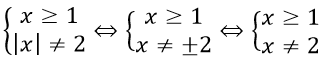

⇒ TXĐ: D = [1; +∞)\{2}.

b) ĐKXĐ: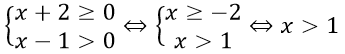

⇒ TXĐ: D = (1; +∞).

c) ĐKXĐ: x² + x + 1 ≠ 0 ⇔ (x + 1/2)² + 3/4 ≠ 0 (đúng ∀ x)

⇒ TXĐ: D = R.

d) ĐKXĐ:

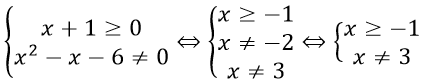
⇒ TXĐ: D = [-1;+∞)\{3}

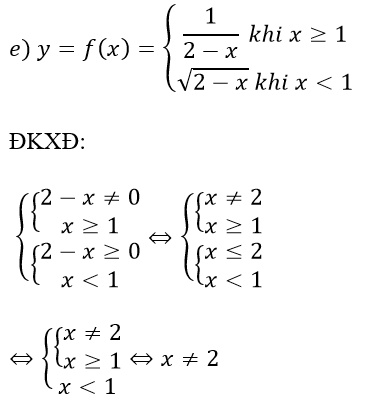
⇒ TXĐ: D = R\{2}

Bài 2:

a) ĐKXĐ: x ≠ m

Hàm số xác định trên (-1; 0) ⇔ m ∉ (-1; 0)

⇔

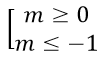
Vậy với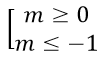thì hàm số xác định trên (-1; 0)

b) ĐKXĐ: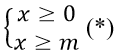

Nếu m > 0 thì (*) ⇔ x ≥ m ⇒ D = [m; +∞) nên m > 0 không thỏa mãn

Nếu m ≤ 0 thì (*) ⇔ x ≥ 0 ⇒ D = [0; +∞)

Vậy m ≤ 0 là giá trị cần tìm.

Bài 3:

a) Hàm số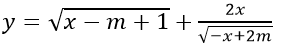xác định trên (-1; 3)

ĐKXĐ: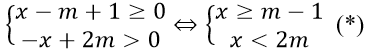

Với m ≤ -1 thì (*) vô nghiệm.

Với m > -1 thì (*) ⇔ m - 1 ≤ x < 2m

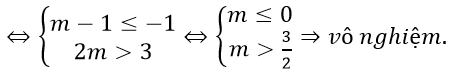
Vậy không tồn tại m thỏa mãn yêu cầu đề bài.

b) Hàm số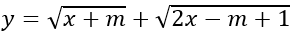xác định trên (0;+∞)

ĐKXĐ: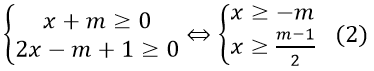

Ta có: (m - 1)/2 > -m ⇔ m > 1/3

Với m > 1/3 thì (2) ⇔ x ≥ (m - 1)/2

⇒ D = [(m - 1)/2; +∞)

Khi đó hàm số xác định trên (0; +∞) khi (m - 1)/2 ≤ 0 ⇔ m ≤ 1

⇒ 1/3 < m ≤ 1

Với m ≤ 1/3 thì (2) ⇔ x ≥ -m ⇒ D = [-m; +∞)

Khi đó hàm số xác định trên (0; +∞) khi -m ≤ 0 ⇔ m ≥ 0

⇒ 0 ≤ m ≤ 1/3

Vậy các giá trị m cần tìm là 0 ≤ m ≤ 1.

Bài 4

a)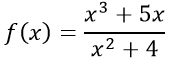

TXĐ: D = R.

Với x ∈ D ⇒ -x ∈ D.Ta có:

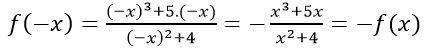
Hàm số đã cho là hàm số lẻ.

b)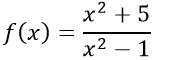

ĐKXĐ: x² - 1 ≠ 0 ⇔ x ≠ ±1 ⇒ TXĐ: D = R\{1; -1}

Với x ∈ D ⇒ -x ∈ D.Ta có:

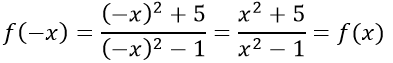
Hàm số đã cho là hàm số chẵn

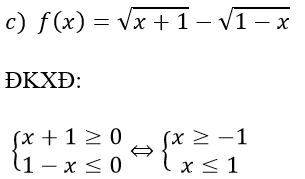
⇒ TXĐ: D = [-1;1]

Với x ∈ D ⇒ -x ∈ D.Ta có:

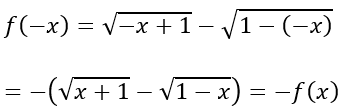
Hàm số đã cho là hàm số lẻ.

d)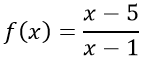

ĐKXĐ: x - 1 ≠ 0 ⇔ x ≠ 1 ⇒ TXĐ: D = R\{1}

Với x₀ = -1 ∈ D ⇒ -x₀ = 1 ∉ D

Vậy hàm số không chẵn cũng không lẻ.

e)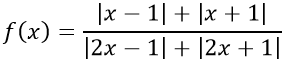

TXĐ: R

Với x ∈ D ⇒ -x ∈ D.Ta có:

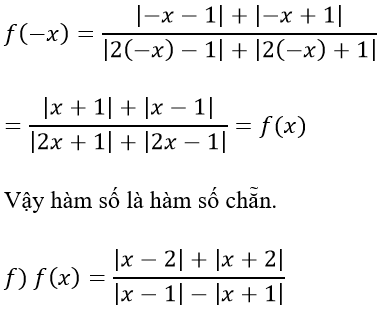
ĐKXĐ: |x - 1| - |x + 1| ≠ 0 ⇔ |x - 1| ≠ |x + 1|

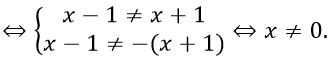
TXĐ: D = R\ {0}

Với x ∈ D ⇒ -x ∈ D.Ta có:

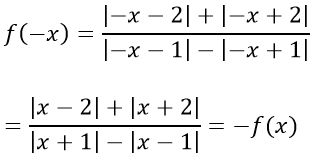
Vậy hàm số đã cho là hàm số lẻ.

Bài 5:

a) Ta có hàm số y = f(x) + g(x) có tập xác định D. Do hàm số y = f(x); y = g(x) lẻ nên ∀ x ∈ D ⇒ -x ∈ D và f(-x) = -f(x); g(-x) = -g(x) suy ra

y(-x) = f(-x)+ g(-x) = -[f(x) + g(x)] = -y(x)

Suy ra hàm số y = f(x) + g(x) là hàm số lẻ.

b) Giả sử hàm số y = f(x) chẵn, y = g(x) lẻ.

Khi đó hàm số y = f(x)g(x) có tập xác định là D nên ∀ x ∈ D ⇒ -x ∈ D

Ta có y(-x)= f(-x)g(-x) = f(x)[-g(x)] = -[f(x)g(x)] = -y(x)

Do đó hàm số y = f(x)g(x) lẻ.

Bài 6

a) Ta có TXĐ: D = R nên ∀ x ∈ D ⇒ -x ∈ D

Đồ thị hàm số đã cho nhận gốc tọa độ O làm tâm đối xứng khi và chỉ khi nó là hàm số lẻ

⇔ f(-x) = -f(x), ∀ x ∈ R.

⇔ (-x)³ - (m² - 9)(-x)² + (m + 3)(-x) + m - 3 = x³ - (m² - 9)x² + (m + 3)x + m - 3, ∀ x ∈ R.

⇔ 2(m² - 9)x² - 2(m - 3) = 0, ∀ x ∈ R.

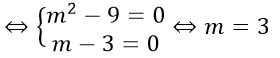
b) Ta có TXĐ: D = R nên ∀ x ∈ D ⇒ -x ∈ D

Đồ thị hàm số đã cho nhận trục tung làm trục đối xứng khi và chỉ khi nó là hàm số chẵn

⇔ f(-x) = f(x), ∀ x ∈ R.

⇔ (-x)⁴ - (m² - 3x + 2)(-x)³ + m² - 1 = x⁴ - (m² - 3x + 2)x³ + m² - 1, ∀ x ∈ R.

⇔ 2(m² - 3x + 2)x³ = 0, ∀ x ∈ R.

⇔ m² - 3x + 2 = 0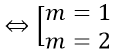

Bài 7:

a) Hàm số đồng biến trên (-∞; 4/3) và nghịch biến trên khoảng (4/3; +∞)

b) Với mọi x₁; x₂ ∈ R; x₁ ≠ x₂ ta có:

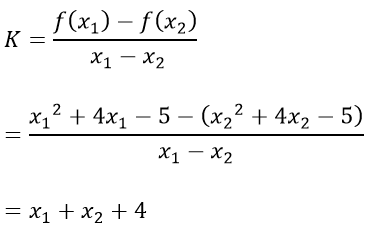
x₁; x₂ ∈ (-∞; -2) ⇒ K < 0 suy ra hàm số nghịch biến trên (-∞; -2).

x₁; x₂ ∈ (-2; +∞) ⇒ K > 0 suy ra hàm số đồng biến trên (-2; +∞).

c) Với mọi x₁; x₂ ∈ R; x₁ ≠ x₂ ta có:

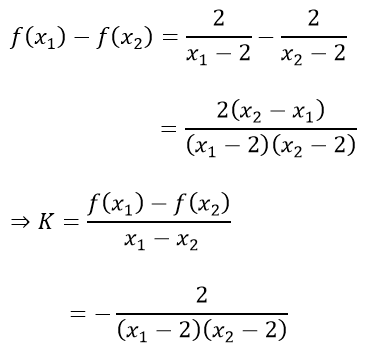
x₁; x₂ ∈ (-∞; 2) ⇒ K < 0 suy ra hàm số nghịch biến trên (-∞; 2).

x₁; x₂ ∈ (2; +∞) ⇒ K > 0 suy ra hàm số đồng biến trên (2; +∞)

d) Với mọi x₁; x₂ ∈ (-∞; 1); x₁ ≠ x₂ ta có:

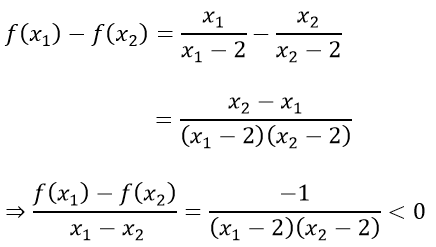
Vậy hàm số nghịch biến trên(-∞; 1).

Bài 8:

Với mọi x₁; x₂ ∈ R; x₁ ≠ x₂ ta có:

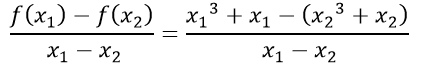
        = x₁² + x₂² + x₁x₂ + 1 > 0

Suy ra hàm số đã cho đồng biến trên R.

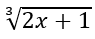
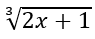
Ta có x³ - x =+ 1 ⇔ x³ + x = 2x + 1 +

Đặt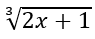= y, phương trình trở thành x³ + x = y³ + y

Do hàm số f(x) = x³ + x đồng biến trên R nên

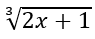
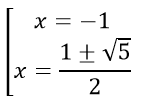
x = y ⇒= x ⇔ x³ - 2x - 1 = 0

⇔

Vậy phương trình có nghiệm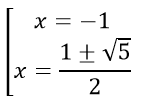

Bài 9: Cho hàm số y = √(x-1) + x² - 2x

a) Với mọi x₁; x₂ ∈ [1; +∞); x₁ ≠ x₂ ta có:

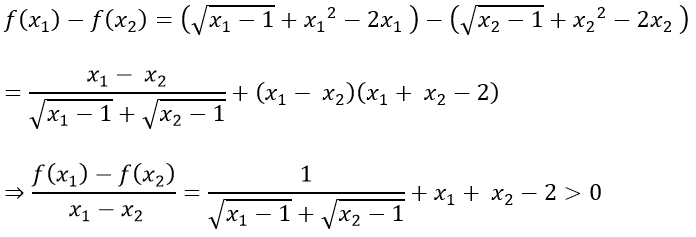
Do đó hàm số đã cho đồng biến trên [1; +∞)

b) Do hàm số đồng biến trên [1; +∞) nên f(2) < f(x) < f(5) ⇔ 1 < f(x) < 17

Vậy giá trị nhỏ nhất của hàm số trên [2; 5] là 1, đạt được khi x = 2.

Vậy giá trị lớn nhất của hàm số trên [2; 5] là 17, đạt được khi x = 5.

Bài 10:

a) Ta có: y = x³ + 2(m-1)x² + (m² - 4m + 1)x - 2(m² + 1)

⇔ m²(x - 2) + m(2x² - 4x) + x³ - 2x² + x - 2 - y = 0

Tọa độ điểm cố định mà họ đồ thị đồ thị luôn đi qua là nghiệm của hệ:

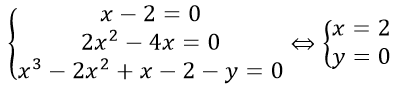
Vậy điểm cần tìm là A (2; 0)

b)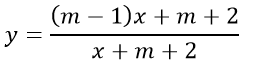

ĐKXĐ: x + m + 2 ≠ 0 ⇔ x ≠ -m - 2

Hàm số tương đương với:

(m - 1)x + m + 2 = y(x + m + 2)

⇔ m(x + 1 - y) - (x - 2 + xy + 2y) = 0

Tọa độ điểm cố định mà họ đồ thị đồ thị luôn đi qua là nghiệm của hệ:

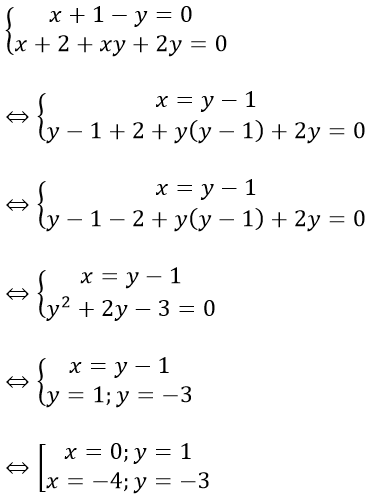
Điểm cố định là (0; 1) và (-4; -3)

Bài 11: Điểm M(1; 0) thuộc đồ thị hàm số đã cho khi và chỉ khi:

f(1) = 0

⇔ 0 = 2 + (m - 1) + (m² - 1) + 2(m² - 3m + 2) - 3

⇔ 3m² - 5m + 1 = 0

⇔

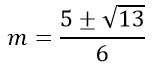
Vậylà giá trị cần tìm.