Cách giải bài tập về đồ thị hàm số lớp 10 hay, chi tiết - Toán lớp 10
Cách giải bài tập về đồ thị hàm số lớp 10 hay, chi tiết
Với Cách giải bài tập về đồ thị hàm số lớp 10 hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập đồ thị hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

1. Phương pháp giải.
Cho hàm số y = f(x) xác định trên D. Đồ thị hàm số f là tập hợp tất cả các điểm M(x;f(x)) nằm trong mặt phẳng tọa độ với x ∈ D.
Chú ý: Điểm M(x0; y0 ) ∈ (C) đồ thị hàm số y = f(x) ⇔ y0 = f(x0 ).
Sử dụng định lý về tịnh tiến đồ thị một hàm số
2. Các ví dụ minh họa.
Ví dụ 1: Cho hai hàm số f(x) = 2x2 + 3x + 1 và
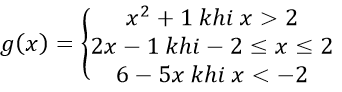
a) Tính các giá trị sau f(-1); g(-3); g(2); g(3)
b) Tìm x khi f(x) = 1.
c) Tìm x khi g(x) = 1.
Hướng dẫn:
a) Ta có:
f(-1) = 2.(-1)2 + 3(-1) + 1 = 0
g(-3) = 6 - 5.(-3) = 21
g(2) = 2.2 - 1 = 3
g(3) = 32 + 1 = 10
b) Ta có f(x) = 1 ⇔ 2x2 + 3x + 1 = 1
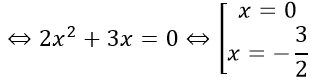
c) Với x > 2 ta có g(x) = 1
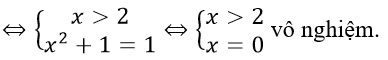
Với -2 ≤ x ≤ 2 ta có g(x) = 1
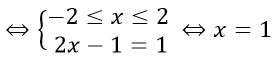
Với x < -2 ta có g(x) = 1
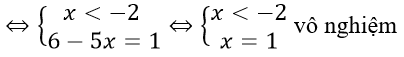
Vậy g(x) = 1 ⇔ x = 1.

Ví dụ 2: Cho hàm số y = mx3 - 2(m2 + 1)x2 + 2m2 - m.
a) Tìm m để điểm M(-1;2) thuộc đồ thị hàm số đã cho
b) Tìm các điểm cố định mà đồ thị hàm số đã cho luôn đi qua với mọi m.
Hướng dẫn:
a) Điểm M(-1; 2) thuộc đồ thị hàm số đã cho khi và chỉ khi
2 = -m - 2(m2 + 1) + 2m2 - m ⇔ m = -2
Vậy m = -2 là giá trị cần tìm.
b) Để N(x;y) là điểm cố định mà đồ thị hàm số đã cho luôn đi qua, điều kiện cần và đủ là
y = mx3 - 2(m2 + 1)x2 + 2m2 - m, ∀m.
⇔ 2m2(1 - x2 ) + m(x3 - 1) - 2x2 - y = 0, ∀m.
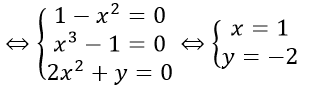
Vậy đồ thị hàm số đã cho luôn đi qua điểm N (1; -2).
Chú ý: Đa thức anxn + an - 1xn - 1 + ... + a1 x + a0 = 0 với mọi x ∈ K khi và chỉ khi an = an - 1 = ... = a1 = a0 = 0.
Ví dụ 3: Tìm trên đồ thị hàm số y = -x3 + x2 + 3x - 4 hai điểm đối xứng nhau qua gốc tọa độ.
Hướng dẫn:
Gọi M, N đối xứng nhau qua gốc tọa độ O. M(x0; y0 ) ⇒ N(-x0; -y0 )
Vì M, N thuộc đồ thị hàm số nên
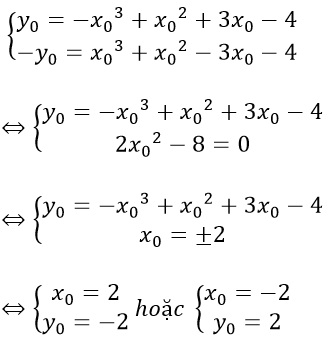
Vậy hai điểm cần tìm có tọa độ là (2; -2) và (-2; 2).

